4. Hình học phi Euclid¶

4.1. Giới thiệu¶

Euclid là một trong những nhà toán học vĩ đại nhất lịch sử loài người, người đã viết quyển Elements, trình bày các mệnh đề làm cơ sở cho hình học, gọi là các tiên đề.

Chúng ta luôn cần một chứng minh để khẳng định hoặc bác bỏ bất kì mệnh đề toán học nào. Thông thường, việc chứng minh mệnh đề sẽ dựa trên các mệnh đề đã đúng trước đó. Tuy nhiên dễ thấy rằng việc truy ngược như vậy không thể thực hiện vô hạn mà phải tới một "điểm neo" nào đó, nghĩa là các mệnh đề đúng không cần chứng minh. Các mệnh đề đó chính là các tiên đề. Tuy nhiên các tiên đề phải đúng, ít nhất là được kiểm nghiệm trên thực tiễn.

Các tiên đề Euclid có năm tiên đề chính. Trong số đó có tiên đề thứ 5, viết số La Mã thành tiên đề V, là rắc rối và thiếu tụ nhiên nhất:

Nếu hai đường thẳng tạo ra với một đường thẳng thứ ba cắt chúng hai góc trong cùng phía có tổng nhỏ hơn hai góc vuông thì khi kéo dài hai đường thẳng đó về phía ấy đến một lúc nào đó chúng sẽ phải cắt nhau.

Tiên đề này có hai điểm kì quái.

Đầu tiên là nó khá dài dòng. Các tiên đề thường là những điều hiển nhiên mà ta thấy được và là cơ sở cho hình học. Do đó tiên đề thường ngắn gọn, chỉ rõ một hiện tượng.

Ví dụ:

qua hai điểm phân biệt trên mặt phẳng chỉ vẽ được một đường thẳng;
đường thẳng kéo dài vô hạn về hai phía;
mọi góc vuông đều bằng nhau.

Điểm kì quái thứ hai là tiên đề này khá rối rắm và chúng ta cần cẩn thận suy xét ý nghĩa của nó. Trong khi đó, như đã nói ở trên, tiên đề chỉ ra những quan sát thực tiễn và là cơ sỏ cho hình học (hoặc bất kì lĩnh vực toán học khác). Do đó tiên đề cần đơn giản, dễ nắm bắt.

Điều thú vị là hệ thống tiên đề của Euclid đã đứng vững 2000 năm mà không có vấn đề gì. Các nhà toán học thời đó, mỗi lần gặp các vấn đề về hình học, sẽ tham khảo các tài liệu do Euclid để lại. Còn có thông tin rằng những nghiên cứu dám nghi ngờ hoặc phản đối hệ tiên đề Euclid sẽ bị các nhà khoa học xung quanh bác bỏ, khá giống với tòa án dị giáo thời Trung Cổ.

Tuy nhiên, ba nhà toán học kiệt xuất đã xây dựng nên hình học phi Euclid độc lập nhau. Hình học phi Euclid không bác bỏ hình học Euclid, mà chúng bổ trợ cho nhau, làm đầy đủ các khía cạnh hình học.

Phần này mình tham khảo từ series Путь к геометрии Лобачевского. Trong tiếng Việt tên series nghĩa là "Đường tới hình học Lobachevsky". Series gồm 6 phần nhưng mình chỉ tham khảo 5 phần đầu. Phần cuối là [TODO] sau này nghiên cứu thêm.

4.2. Sự ra đời hình học phi Euclid¶

Tiên đề V có vẻ rối rắm và dài dòng. Do đó nhiều nhà toán học cũng nghĩ rằng, có khi nào đây là một định lý chứ không phải tiên đề không? Như vậy họ đã cố gắng chứng minh tiên đề V bằng các tiên đề còn lại. Kết quả là họ ... thất bại.

Nhà toán học người Nga Lobachevsky có một cách tiếp cận khác. Ông này kiểu: "Hmm, giả sử mình thay tiên đề này bởi phủ định của nó rồi đi chứng minh các định lý hình học thì có khi nào phát sinh mâu thuẫn không nhỉ?". Nghĩa là ông ấy giữ nguyên tất cả tiên đề Euclid trừ tiên đề V, và thay tiên đề V thành phủ định của nó, rồi đi chứng minh các định lý hình học và hy vọng tìm ra mâu thuẫn toán học nào đó.

Kết quả là Lobachevsky đã thất bại (trong việc tìm ra mâu thuẫn).

Ông đã chứng minh hàng chục định lý mà không phát hiện điều gì bất thường.

Nếu vậy, phải chăng hình học phi Euclid khi thay tiên đề V bởi phủ định của nó, cũng chặt chẽ như hìnhh học Euclid?

Phần sau mình sẽ đề cập tới hình học phi Euclid trong hệ tọa độ, cụ thể là các mặt cong trên nền tảng hình học Lobachevsky.

4.3. Tích vô hướng trong không gian Euclide¶

Với hai vector $\bm{x} = (x_1, x_2, x_3)$ và $\bm{y} = (y_1, y_2, y_3)$, tích vô hướng của hai vector được định nghĩa là

\[\langle \bm{x}, \bm{y} \rangle = x_1 y_1 + x_2 y_2 + x_3 y_3.\]

Độ dài của vector $\bm{x}$, kí hiệu là $\lVert \bm{x} \rVert$ và được tính bởi công thức

\[\lVert \bm{x} \rVert = \sqrt{\langle \bm{x}, \bm{x} \rangle}.\]

Khoảng cách giữa hai điểm $A = \bm{x} = (x_1, x_2, x_3)$ và $B = \bm{y} = (y_1, y_2, y_3)$ là

\[AB = d(\bm{x}, \bm{y}) = \lVert \bm{x} - \bm{y} \rVert.\]

4.4. Độ dài đường cong trong không gian Euclide¶

Trong bài viết về tích phân đường mình đã tìm công thức tính độ dài đường trên mặt phẳng Euclide. Khi đó, nếu đường cong $\gamma$ xác định các tọa độ bởi tham số $t$, nghĩa là

\[\begin{split}\gamma(t) = \begin{cases} x = x(t) \\ y = y(t) \end{cases}\end{split}\]

thì độ dài đường cong từ $t_0$ tới $t_1$ (tức là $t_0 \leqslant t \leqslant t_1$) là tích phân

\[\boxed{l(\gamma) = \int_\gamma dl = \int_{t_0}^{t_1} \sqrt{dx^2 + dy^2} = \int_{t_0}^{t_1} \sqrt{(x'(t))^2 + (y'(t))^2} \, dt.}\]

Tương tự, đối với đường cong trong không gian Euclide $Oxyz$ có tọa độ là hàm số theo tham số $t$, nghĩa là

\[\begin{split}\gamma(t) = \begin{cases} x = x(t) \\ y = y(t) \\ z = z(t) \end{cases}\end{split}\]

thì độ dài đường cong từ $t_0$ tới $t_1$ là tích phân

\[\boxed{l(\gamma) = \int_\gamma dl = \int_{t_0}^{t_1} \sqrt{dx^2 + dy^2 + dz^2}.}\]

Ở đây một biểu thức quan trọng sẽ được sử dụng xuyên suốt về sau là

\[dl = \sqrt{dx^2 + dy^2 + dz^2},\]

nhưng chúng ta sẽ bình phương để dễ tính toán

\[\boxed{dl^2 = dx^2 + dy^2 + dz^2.}\]

Nếu chúng ta có nhiều tham số thì sử dụng công thức đạo hàm riêng. Giả sử $x = x(u, v)$ và $y = y(u, v)$ thì

\[\begin{split}dx & = \dfrac{\partial x}{\partial u} du + \dfrac{\partial x}{\partial v} dv = \dots \\ dy & = \dfrac{\partial y}{\partial u} du + \dfrac{\partial y}{\partial v} dv = \dots \\ dz & = \dfrac{\partial z}{\partial u} du + \dfrac{\partial z}{\partial v} dv = \dots\end{split}\]

Khi đó

\[\boxed{dl^2 = \left(a(u, v) du + b(u, v) dv\right)^2.}\]

4.5. Mặt cầu¶

Mặt cầu là tập hợp các điểm cách một điểm cố định một khoảng không đổi trong không gian.

Mặt cầu tâm $O(x_0, y_0, z_0)$ với bán kính $r$ là tập hợp các điểm $M(x, y, z)$ thỏa phương trình

\[(x - x_0)^2 + (y - y_0)^2 + (z - z_0)^2 = r^2.\]

Chúng ta sẽ đưa tâm mặt cầu về gốc tọa độ $O(0, 0, 0)$ để thuận tiện tính toán về sau. Phương trình sẽ trở thành

\[x^2 + y^2 + z^2 = r^2.\]

Một cách khác để biểu diễn các điểm của mặt cầu là sử dụng tọa độ cầu, nghĩa là biểu diễn tọa độ $(x, y, z)$ thông qua hai tham số $(\theta, \phi)$ (ở đây không có $r$ vì bán kính đã cố định rồi). Khi đó, tọa độ sẽ có dạng

\[\begin{split}\begin{cases} x = r \sin\theta \cos\phi \\ y = r \sin\theta \sin\phi \\ z = r \cos\theta, \end{cases},\end{split}\]

trong đó $0 \leqslant \theta, \phi \leqslant 2\pi$.

4.6. Khoảng cách giữa hai điểm trên mặt cầu¶

Trên mặt phẳng, khoảng cách giữa hai điểm là độ dài phần đường thẳng nằm giữa hai điểm đó. Tuy nhiên, trên mặt cầu thì không phải là đường thẳng mà chúng ta thường biết nữa.

Sử dụng công thức về độ dài đường cong bên trên có thể xác định được khoảng cách giữa hai điểm trên mặt cầu (trong tọa độ cực) là

\[\begin{split}dx & = r\cos\theta\cos\phi \ d\theta - r\sin\theta\sin\phi \ d\phi \\ dy & = r\cos\theta\sin\phi \ d\theta + r\sin\theta\cos\phi \ d\phi \\ dz & = -r \sin\theta \ d\theta\end{split}\]

Từ đây ta suy ra

\[dl^2 = dx^2 + dy^2 + dz^2 = r^2(d\theta^2 + \sin^2\theta \ d\phi^2).\]

Ví dụ, mình muốn tính độ dài đường xích đạo, là vòng có độ dài lớn nhất trên mặt cầu, ứng với $\theta = \pi / 2$ và $0 \leqslant \phi \leqslant 2\pi$, theo công thức trên

\[\sin\dfrac{\pi}{2} = 1, \quad d\theta = 0,\]

nên

\[l(\gamma) = \int dl = \int r \sqrt{0^2 + \sin^2(\pi / 2) \, d\phi^2} = \int_{0}^{2\pi} r d\phi = 2\pi r.\]

4.7. Đường thẳng trên mặt cầu¶

Mỗi mặt phẳng nếu cắt mặt cầu sẽ được một "đường". Đường đó là tập hợp các điểm thỏa mãn hệ phương trình

\[\begin{split}\begin{cases} x^2 + y^2 + z^2 = 1 \\ ax + by + cz = 0. \end{cases}\end{split}\]

Ở đây lấy đường tròn đơn vị và mặt phẳng đi qua gốc tọa độ cho đơn giản, $(a, b, c)$ là các số cố định.

Khi đó hệ tọa độ cầu sẽ là

\[\begin{split}x & = \cos\phi \cos t - \sin\phi \sin t \cos t \\ y & = \sin\phi \sin t \cos \theta \\ z & = \sin t \sin \theta.\end{split}\]

Trong đó $\theta$ và $\phi$ cố định, còn $t$ thay đổi từ $0$ tới $2\pi$ trên vòng tròn cắt.

Trên mặt cầu không tồn tại hai đường song song.

4.8. Phép chiếu lập thể¶

Phép chiếu lập thể (Stereographic projection, Стереографическая проекция) là phép chiếu mặt cầu lên mặt phẳng.

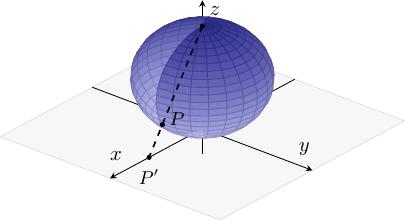
Ở hình trên, xét mặt cầu

\[x^2 + y^2 + (z - 1)^2 = 1\]

và mặt phẳng $z = 0$.

Chọn điểm cực bắc $I(0, 0, 2)$ làm tâm phép chiếu. Khi đó, phép chiếu lập thể biến mỗi điểm $P$ thuộc mặt cầu thành điểm $P'$ thuộc mặt phẳng chiếu sao cho $I$, $P$ và $P'$ thẳng hàng. Nói cách khác, $P'$ là giao điểm của đường thẳng $IP$ và mặt phẳng chiếu.

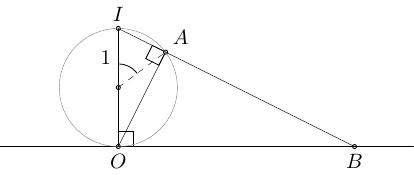
Trong trường hợp này, khi chiếu một vòng tròn song song mặt phẳng lên mặt phẳng ta được hình tròn. Lúc này, góc $\phi$ sẽ không thay đổi khi chiếu lên mặt phẳng, nhưng bán kính sẽ thay đổi, không phải là bán kính mặt cầu ban đầu.

Để tìm bán kính hình tròn ở mặt phẳng chiếu, trong tam giác vuông $IOB$ ta có

\[OB = IO \cdot \cot\angle IBO = IO \cdot \cot\angle IOA = IO \cdot \cot\left(\dfrac{\angle ICA}{2}\right) = IO \cdot \cot\dfrac{\theta}{2}.\]

Một công thức lượng giác quen thuộc

\[\cos^2\alpha = \dfrac{1 + \cos 2\alpha}{2}, \ \sin^2\alpha = \dfrac{1 - \cos 2\alpha}{2},\]

suy ra

\[\cot^2\alpha = \dfrac{\cos^2\alpha}{\sin^2\alpha} = \dfrac{(1 + \cos 2\alpha)/2}{(1 - \sin 2\alpha)/2} = \dfrac{1+\cos 2\alpha}{1-\cos 2\alpha}.\]

Như vậy

\[\cot \dfrac{\theta}{2} = \sqrt{\dfrac{1 + \cos\theta}{1 - \cos\theta}}\]

và thay $IO = 2$ vào ta có

\[\begin{split}\begin{cases} r = 2 \sqrt{\dfrac{1 + \cos\theta}{1 - \cos\theta}} = OB \\ \phi' = \phi \end{cases}\end{split}\]

là các tham số của ảnh trên mặt phẳng qua phép chiếu lập thể. Tọa độ của điểm trên mặt phẳng chiếu là

\[\begin{split}\begin{cases} u = r \cos\phi' = r(\theta)\cos\phi \\ v = r\sin\phi' = r(\theta)\sin\phi. \end{cases}\end{split}\]

Ở trên, bình phương độ dài đường cong trên mặt cầu được tính theo vi phân

\[dl^2 = dx^2 + dy^2 + dz^2\]

và ở tọa độ cầu là

\[dl^2 = d\theta^2 + \sin^2\phi \, d\phi^2\]

với $r = 1$.

Bây giờ chúng ta tìm cách thay $d\theta$ và $d\phi$ từ kết quả phép chiếu lập thể vào bình phương vi phân đường cong. Để làm điều đó thì cần biểu diễn ngược lại $\theta$ theo $r$, còn $\phi' = \phi$ nên không cần xét tới.

Ta có

\[r = 2\sqrt{\dfrac{1 + \cos\theta}{1 - \cos\theta}} \Longrightarrow \cos\theta = \dfrac{r^2-4}{r^2+4} \Longleftrightarrow \theta = \arccos\left(\dfrac{r^2-4}{r^2+4}\right).\]

Lúc này, đạo hàm của $\arccos(x) = -\dfrac{1}{\sqrt{1 - x^2}}$ nên mình suy ra

\[\begin{split}d\theta & = -\dfrac{1}{\sqrt{1 - \left(\dfrac{r^2-4}{r^2+4}\right)^2}} \cdot \left(\dfrac{r^2-4}{r^2+4}\right)' \ dr\\ & = -\dfrac{1}{\dfrac{1}{r^2+4} \cdot \sqrt{(r^2 + 4)^2 - (r^2 - 4)^2}} \cdot \dfrac{2r(r^2 + 4) - 2r(r^2 - 4)}{(r^2+4)^2} \ dr \\ & = -\dfrac{16r}{(r^2+4) \cdot \sqrt{16r^2}} \ dr.\end{split}\]

Bình phương hai vế suy ra

\[d\theta^2 = \dfrac{16}{(r^2+4)^2} \ dr^2.\]

Tương tự, với $\sin^2\theta \ d\phi^2$ thì ta thay biểu diễn $\cos\theta$ theo $r$ bên trên vào

\[\sin^2\theta = 1 - \cos^2\theta = 1 - \left(\dfrac{r^2-4}{r^2+4}\right)^2 = \dfrac{16r^2}{(r^2+4)^2}.\]

Như vậy ta có

\[dl^2 = \dfrac{16}{(r^2+4)^2} (dr^2 + r^2 \ d\phi^2).\]

Ở trên chúng ta muốn dời tọa độ $(r, \phi)$ sang tọa độ $(u, v)$ với

\[\begin{split}\begin{cases} u = r\cos\phi \\ v = r\sin\phi \end{cases} \Longleftrightarrow \begin{cases} r^2 = u^2 + v^2 \\ \phi = \arctan\dfrac{u}{v} \end{cases}\end{split}\]

và

\[dl^2 = \dfrac{16}{(u^2 + v^2 + 4)^2}(du^2 + dv^2).\]

Câu hỏi. Ảnh của các đường thẳng trên mặt cầu (các vòng tròn lớn) lên mặt phẳng là gì?

Trả lời. Đối với các đường không đi qua cực bắc (điểm $I$) thì ảnh là hình tròn, còn các đường đi qua cực bắc thì ảnh là đường thẳng đi qua gốc tọa độ.

[TODO] Tìm phương trình của hình chiếu.

4.9. Không gian giả Euclid¶

Trong không gian Euclid, tích vô hướng của hai vector $\bm{x} = (x_1, x_2, x_3)$ và $\bm{y} = (y_1, y_2, y_3)$ là

\[\mathbb{R}^3: \langle \bm{x}, \bm{y} \rangle = x_1 y_1 + x_2 y_2 + x_3 y_3.\]

Trong không gian giả Euclid, tích vô hướng sẽ là

\[\mathbb{R}_1^3: \langle \bm{x}, \bm{y} \rangle = -x_1 y_1 + x_2 y_2 + x_3 y_3.\]

Như vậy, độ dài vector $\lVert \bm{x} \rVert^2 = \langle \bm{x}, \bm{x} \rangle$ trong không gian giả Euclid có thể là số âm.

4.10. Giả cầu (Pseudosphere)¶

Dễ thấy rằng do mặt cầu là tập hợp các điểm cách điểm cố định một đoạn không đổi $r$ nên cũng tương đương với mặt cầu là tập các vector có độ dài bằng $r$, nghĩa là

\[S^2 = \{ \bm{x} : \langle \bm{x}, \bm{x} \rangle = r^2 \} \subset \mathbb{R}^3.\]

Bây giờ ta định nghĩa giả cầu là tập các điểm thỏa phương trình

\[-x^2 + y^2 + z^2 = -r^2,\]

hay tương đương là

\[L^2 = \{ \bm{x} : \langle \bm{x}, \bm{x} \rangle = -r^2 \} \subset \mathbb{R}_1^3.\]

Để tham số hóa giả cầu chúng ta cần thống nhất hệ thống tọa độ trong không gian giả Euclid $\mathbb{R}_1^3$:

Tích vô hướng trong $\mathbb{R}_1^3$ là

\[\langle \bm{x}, \bm{y} \rangle = -x_1 y_1 + x_2 y_2 + x_3 y_3.\]

Độ dài vector (chuẩn Euclid) vẫn là tích vô hướng của chính nó

\[\lVert \bm{x} \rVert = \langle \bm{x}, \bm{x} \rangle.\]

Vi phân độ dài đường cong

\[dl^2 = \lVert (dx, dy, dz) \rVert = -dx^2 + dy^2 + dz^2.\]

Tiếp theo chúng ta sẽ biểu diễn giả cầu trong tọa độ cực

\[\begin{split}L^2 = \begin{cases} x = \cosh u \\ y = \sinh u \cos\theta \\ z = \sinh u \sin\theta \end{cases}\end{split}\]

Ở đây các công thức có vẻ hơi lạ vì không phải các hàm lượng giác (trigonometric functions) như chúng ta hay gặp, mà là các hàm hyperbol (hyperbolic function) được định nghĩa như sau:

\[\sinh x = \dfrac{e^x - e^{-x}}{2}, \quad \cosh x = \dfrac{e^x + e^{-x}}{2}.\]

Như vậy ta có thể tìm được các vi phân

\[\begin{split}dx & = \dfrac{\partial x}{\partial u} \, du + \dfrac{\partial x}{\partial \theta} \, d\theta = \sinh u \, du \\ dy & = \dfrac{\partial y}{\partial u} \, du + \dfrac{\partial y}{\partial \theta} \, d\theta = \cosh u \cos\theta\,du - \sinh u \sin\theta \,d\theta \\ dz & = \dfrac{\partial z}{\partial u} \, du + \dfrac{\partial z}{\partial \theta} \, d\theta = \cosh u \sin\theta\,du + \sinh u\cos\theta\,d\theta\end{split}\]

Như vậy ta có

\[\boxed{dl^2 = -dx^2 + dy^2 + dz^2 = du^2 + \sinh^2 u\,d\theta,}\]

ở đây lưu ý là

\[\cosh^2 u - \sinh^2 u = \dfrac{(e^u + e^{-u})^2 - (e^u - e^{-u})^2}{4} = \dfrac{4 e^u e^{-u}}{4} = 1.\]

Tương tự, bây giờ, vòng tròn lớn trong không gian giả Euclid là giao giữa mặt phẳng và giả cầu, tức là

\[\{ -x^2 + y^2 + z^2 = -1, ax + by + cz = 0 \}\]

với $a$, $b$, $c$ cố định.

4.11. Phép chiếu lập thể trên giả cầu¶

Khi chúng ta cắt giả cầu với một mặt phẳng (lát cắt), ví dụ $z = 0$, chúng ta sẽ thấy một đường hyperbol.

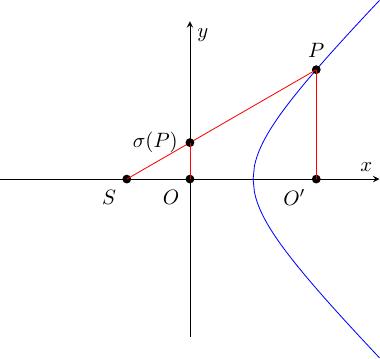
Hình trên là phép chiếu lên mặt phẳng $x = 0$ và chúng ta đang nhìn từ trên xuống (theo hướng $z = 0$).

Kí hiệu phép chiếu lập thể tâm $S$ biến điểm $P$ trên giả cầu thành điểm $\sigma(P)$. Lúc này chúng ta sẽ thiết lập ánh xạ $\sigma: (x, y, z) \to (u, v)$ với $(x, y, z) \in L^2$ là điểm thuộc giả cầu.

Trong trường hợp này các thông số ban đầu là

\[\begin{split}& S = (-1, 0, 0), \\ & P = (x, y, z), \\ & -x^2 + y^2 + z^2 = -1, \\ & \sigma(P) = (u, v).\end{split}\]

Đầu tiên phương trình tham số của đường thẳng $SP$ là

\[\begin{split}\begin{cases} x = x(t) = -1 + (x + 1) t \\ y = y(t) = y t \\ z = z(t) = z t \end{cases}\end{split}\]

Đường thẳng $SP$ cắt mặt phẳng $x = 0$ tại $x(t_0) = 0$, như vậy

\[-1 + (x + 1) t_0 = 0 \Longleftrightarrow t_0 = \dfrac{1}{x + 1} \Longrightarrow (y, z)(t_0) = \left(\dfrac{y}{x + 1}, \dfrac{z}{x+1}\right).\]

Lúc này tọa độ $(u, v)$ chính là $(y, z)(t_0)$, nói cách khác

\[\begin{split}(y, z)(t_0) = (u, v) \Longrightarrow \begin{cases} y = (x + 1) u \\ z = (x + 1) v \end{cases}\end{split}\]

Bây giờ thay ngược $y$ và $z$ vào biểu thức giả cầu (hyperbolic) ta được

\[\begin{split}& -x^2 + y^2 + z^2 = -1 \\ & -x^2 + (x+1)^2 u^2 + (x+1)^2 v^2 = -1 \\ & -x^2 + (x+1)^2 (u^2 + v^2) + 1 = 0 \\ & -x^2 + (x^2 + 2x + 1)(u^2 + v^2) + 1 = 0 \\ & (u^2 + v^2 - 1) x^2 + 2(u^2 + v^2) x + (u^2 + v^2 + 1) = 0\end{split}\]

Xem đây là phương trình bậc hai theo $x$, tính delta ta có

\[\Delta' = (u^2 + v^2)^2 - (u^2 + v^2 - 1)(u^2 + v^2 + 1) = (u^2 + v^2)^2 - ((u^2+v^2)^2 - 1) = 1.\]

Nghiệm của phương trình bậc hai khi đó là

\[x_{1, 2} = \dfrac{-(u^2 + v^2) \pm 1}{u^2 + v^2 - 1}.\]

Như vậy

\[x_1 = -1, \ x_2 = \dfrac{1 + u^2 + v^2}{1 - u^2 - v^2}.\]

Nghiệm thứ hai cho phép biểu diễn $y$ và $z$ theo $u$ và $v$:

\[\begin{split}x + 1 = & \dfrac{1 + u^2 + v^2}{1 - u^2 - v^2} + 1 = \dfrac{2}{1 - u^2 - v^2} \\ \Longrightarrow & \begin{cases} x = \dfrac{1 + u^2 + v^2}{1 - u^2 - v^2} \\ y = (x + 1) u = \dfrac{2u}{1 - u^2 - v^2} \\ z = (x + 1) v = \dfrac{2v}{1 - u^2 - v^2} \end{cases}\end{split}\]

Bây giờ chúng ta đã có thể tính được độ dài hình chiếu. Đầu tiên ta vi phân các biến $x$, $y$ và $z$ theo $u$ và $v$:

\[\begin{split}dx & = \dfrac{\partial x}{\partial u} du + \dfrac{\partial x}{\partial v} dv = \dfrac{4u \, du + 4v \, dv}{(1 - u^2 - v^2)^2} \\ dy & = \dfrac{\partial y}{\partial u} du + \dfrac{\partial y}{\partial v} dv = \dfrac{2(1 + u^2 - v^2)}{(1 - u^2 - v^2)^2} du + \dfrac{4uv}{(1 - u^2 - v^2)^2} dv \\ dz & = \dfrac{\partial z}{\partial u} du + \dfrac{\partial z}{\partial v} dv = \dfrac{4uv}{(1 - u^2 - v^2)^2} du + \dfrac{2(1 - u^2 + v^2)}{(1 - u^2 - v^2)^2} dv\end{split}\]

Khi đó bình phương vi phân đường cong $dl^2$ là

\[\begin{split}(1 - u^2 - v^2)^4 \, dl^2 & = (1 - u^2 - v^2)^4 \cdot (-dx^2 + dy^2 + dz^2) \\ & = -(4u \, du + 4v \, dv)^2 + \left(2(1 + u^2 - v^2) \, du + 4uv \, dv\right)^2 + \left(4uv \, du + 2 (1 + v^2 - u^2) \, dv\right)^2 \\ & = (-16u^2 + 4 (1 + u^2 - v^2)^2 + 16 u^2 v^2) \, du^2 \\ & + (-32 uv + 16uv(1 + u^2 - v^2) + 16uv(1 - u^2 + v^2)) \, dudv \\ & + (-16v^2 + 16u^2v^2 + 4(1 - u^2 + v^2)^2) \, dv^2 \\ & = 4 (1 - u^2 - v^2)^2 \, du^2 + 0 \, dudv + 4 (1 - u^2 - v^2)^2 \, dv^2\end{split}\]

Như vậy thu được

\[dl^2 = \dfrac{4}{(1 - u^2 - v^2)^2}(du^2 + dv^2).\]

4.12. Cách xây dựng của Poincare¶

Xét đường thẳng $xx'$. Đường thẳng $xx'$ chia mặt phẳng làm hai phần, ta gọi là nửa trên và nửa dưới.

Bây giờ ta xây dựng các đối tượng phi Euclid sau:

Điểm phi Euclid là tất cả điểm ở nửa mặt phẳng trên chia bởi $xx'$ nhưng không tính các điểm trên $xx'$
Đường thẳng phi Euclid là mọi nửa đường thẳng vuông góc với $xx'$ và nửa đường tròn tâm nằm trên $xx'$ không tính các điểm nằm trên $xx'$.
Nửa mặt phẳng trên chia bởi đường thẳng $xx'$ được gọi là mặt phẳng phi Euclid.

Cách xây dựng này thỏa mãn các tiên đề Euclid (trừ tiên đề V):

qua hai điểm phân biệt chỉ vẽ được một đường thẳng: với hai điểm $A$ và $B$ bất kì thuộc mặt phẳng phi Eulicd, nếu $AB perp xx'$ thì ta vẽ đường thẳng $AB$, ngược lại ta vẽ đường trung trực của $AB$ cắt $xx'$ tại $I$ và vẽ đường tròn tâm $I$, bán kính $IA$. Như vậy các đường thẳng được xác định duy nhất
đường thẳng kéo dài vô hạn về hai phía: trong hai trường hợp, đường thẳng tiệm cận $xx'$ nhưng không chạm vào $xx'$. Do đó đường thẳng kéo dài vô hạn về $xx'$ (tương tự việc chứng minh đoạn $(0; 1)$ có điểm bằng với $\mathbb{R}$ của Cantor).

Từ hình vẽ trên có thể thấy có nhiều hơn một đường thẳng song với $(d_2)$ mà đi qua điểm $C$ là đường tròn màu cam và đường tròn màu xanh nước suối.

Trong trường hợp này, tổng ba góc của tam giác có thể có số đo tùy ý, thậm chí bằng $0$. Trên hình vẽ, tam giác tạo bởi $A_1$, $A_2$ và $A_3$, giới hạn bởi các đường tròn màu hường, màu xanh lá cỏ và màu xanh nước suối, tạo thành tam giác có tổng ba góc bằng $0$.