4.1. Linear Feedback Shift Register¶

Linear Feedback Shift Register (LFSR) là một ứng dụng quan trọng của hàm boolean để sinh ra một chuỗi các giá trị (giả ngẫu nhiên, pseudorandom).

4.1.1. Linear Feedback Shift Register¶

Xét hàm boolean $n$ biến $f(x_0, x_1, \ldots, x_{n-1})$. Khi đó với các giá trị (bit) khởi tạo $x_0$, $x_1$, ..., $x_{n-1}$ thuộc $\mathbb{F}_2$, ta có thể sinh ra bit ở các vị trí tiếp theo

\[x_{n} = f(x_0, x_1, \ldots, x_{n-1}).\]

Tương tự:

\[x_{n+1} = f(x_1, x_2, \ldots, x_n), \ x_{n+2} = f(x_2, x_3, \ldots, x_{n+1}), \ x_{n+3} = f(x_3, x_4, \ldots, x_{n+2}), \ldots\]

Tổng quát, để sinh bit thứ $n+i$ thì đầu vào sẽ là các bit $x_i$, $x_{i+1}$, ..., $x_{i+n-1}$.

\[x_{n+i} = f(x_i, x_{i+1}, \ldots, x_{i+n-1}).\]

Theo Hình 4.2, kết quả của hàm $f$ sẽ được nối vào sau của dãy bit. Theo đó dãy bit sẽ luôn có dạng $x_0$, $x_1$, ..., $x_n$, ...

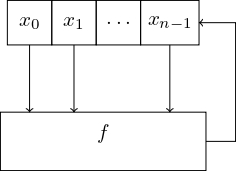
../../_images/lfsr-1.jpg — Hình 4.2 Feedback Shift Register¶

Thông qua hàm $f$, các vector trong $\mathbb{F}_2^n$ sẽ chuyển trạng thái lẫn nhau theo công thức

\[(x_{n-1}, x_{n-2}, \ldots, x_1, x_0) \to (x_n, x_{n-1}, \ldots, x_2, x_1).\]

Ví dụ 4.1

Xét hàm boolean $f(x_3, x_2, x_1, x_0) = x_3 x_2 \oplus x_0$. Bảng chân trị của hàm $f$ là

\[f(x_3, x_2, x_1, x_0) = (0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 0, 1, 0).\]

Ví dụ, với $(0, 0, 0, 1)$, ta có $f(0, 0, 0, 1) = 1$ nên $(0, 0, 0, 1)$ biến đổi thành $(1, 0, 0, 0)$. Như vậy chúng ta có các chuyển đổi đối với hàm $f$ được thể hiện thành $4$ chu trình ở các hình bên dưới.

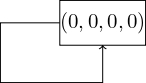
../../_images/lfsr-2.jpg — Hình 4.3 Chu trình thứ nhất của $f$¶

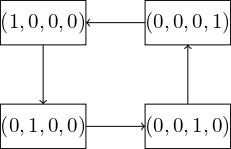
../../_images/lfsr-3.jpg — Hình 4.4 Chu trình thứ hai của $f$¶

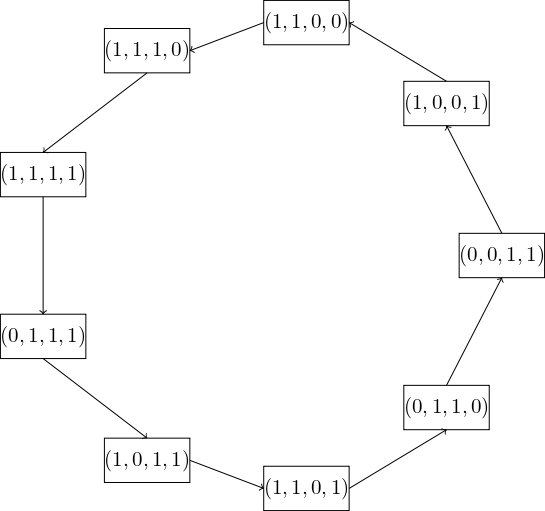
../../_images/lfsr-4.jpg — Hình 4.5 Chu trình thứ ba của $f$¶

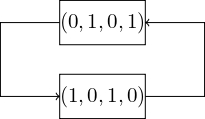
../../_images/lfsr-5.jpg — Hình 4.6 Chu trình thứ tư của $f$¶

Ta thấy rằng tập các vector $\bm{x} = (x_i, x_{i+1}, \ldots, x_{i+n-1})$ có $2^n$ trường hợp. Do đó sẽ có một lúc nào đó (số $i$ nào đó) mà vector $\bm{x}$ trở lại đúng vector ban đầu. Như vậy tồn tại $i$ sao cho

\[(x_0, x_1, \ldots, x_{n-1}) = (x_i, x_{i+1}, \ldots, x_{i+n-1}).\]

Từ đó dãy bit tiếp theo được sinh ra sẽ giống hệt trước đó nên số $i$ nhỏ nhất thỏa mãn đẳng thức được gọi là chu kì của Feedback Shift Register.

Trong các hàm boolean thì hàm boolean tuyến tính được quan tâm nhiều nhất để sinh ra chuỗi bit Feedback Shift Register. Do đó từ đây ta tập trung vào các hàm boolean tuyến tính và Linear Feedback Shift Register.

Nhắc lại, hàm boolean tuyến tính là hàm boolean có dạng

\[f(x_0, x_1, \ldots, x_{n-1}) = a_0 x_0 \oplus a_1 x_1 \oplus \ldots \oplus a_{n-1} x_{n-1}.\]

Trong đó $a_i \in \mathbb{F}_2$ là các hệ số cho trước. Ta định nghĩa đa thức đặc trưng cho hàm boolean tuyến tính như sau.

Định nghĩa 4.9 (Đa thức đặc trưng)

Xét hàm boolean tuyến tính

\[f(x_0, x_1, \ldots, x_{n-1}) = a_0 x_0 \oplus a_1 x_1 \oplus \ldots \oplus a_{n-1} x_{n-1}.\]

Khi đó đa thức đặc trưng tương ứng với hàm $f$ là đa thức có hệ số trong $\mathbb{F}_2$

\[P(x) = a_0 + a_1 x + \ldots + a_{n-1} x^{n-1} + x^n.\]

Do hàm boolean tuyến tính có tính chất là $f(bm{0}) = 0$ nên chu kì tối đa có thể đạt được là $2^n - 1$. Ta có một vài định nghĩa sau để một LFSR đạt được chu kì tối đa.

Định nghĩa 4.10 (Đa thức primitive)

Xét đa thức

\[P(x) = a_0 + a_1 x + \ldots + a_{n-1} x^{n-1} + x^n\]

thuộc $\mathbb{F}_{2^n}$. Ta đã biết trường $\mathbb{F}_{2^n}$ có $2^n - 1$ phần tử khác không. Đặt $p = 2^n - 1$. Đa thức $P(x)$ được gọi là primitive khi với mọi ước nguyên tố $q$ của $p$ thì:

\[x^s \not\equiv 1 \bmod{P(x)}, \quad \text{với} \ s = \frac{p}{q} = \frac{2^n - 1}{q}.\]

Định nghĩa 4.11 (Đa thức đặc trưng với chu kì cực đại)

Đa thức

\[P(x) = a_0 + a_1 x + \ldots + a_{n-1} x^{n-1} + x^n\]

được gọi là đa thức đặc trưng với chu kì cực đại nếu đa thức đó tối giản và là đa thức primitive.

Ví dụ 4.2

Xét đa thức $f(x) = x^4 + x^3 + 1$. Ta có thể xác định xem đa thức này có sinh ra LFSR với chu kì tối đa hay không mà không cần tìm đồ thị chuyển trạng thái của LFSR.

Đầu tiên ta chứng minh $f(x)$ là đa thức tối giản. Thật vậy, giả sử ngược lại, $f(x)$ là tích của hai đa thức bậc nhỏ hơn $4$. Hai trường hợp có thể xảy ra là $f(x)$ chia hết cho đa thức tối giản bậc $1$ hoặc bậc $2$.

Các đa thức tối giản bậc $1$ là $x$ và $x+1$. Ta có thể kiểm chứng rằng $f(x)$ không chia hết cho bất kì đa thức nào ở trên. Tương tự, đa thức tối giản bậc $2$ (trong $\mathbb{F}_{2^4}$) là $x^2 + x + 1$ và $f(x)$ cũng không chia hết cho đa thức này. Như vậy ta có thể kết luận rằng $f(x)$ là đa thức tối giản.

Trong $\mathbb{F}_{2^4}$ có $2^4 - 1 = 15$ phần tử khác $0$. Các ước nguyên tố của $15$ là $3$ và $5$. Ta thấy rằng

\[x^3 \not\equiv 1 \ \text{và} \ x^5 = x \cdot x^4 = x \cdot (x^3 + 1) = x^4 + x = x^3 + x + 1 \not\equiv 1.\]

Như vậy $f(x)$ là đa thức primitive.

Như vậy ta có thể kết luận rằng đa thức $f(x)$ sinh ra LFSR với chu kì tối đa.

4.1.2. Thuật toán Berlekamp-Massey¶

Thuật toán Berlekamp-Massey là thuật toán tìm đa thức sinh có chu kì ngắn nhất sinh ra một dãy LFSR cho trước.

Bài toán ở đây là, giả sử chúng ta có một dãy bit

\[u_0, u_1, \ldots, u_{l-1}\]

là một dãy bit được sinh giả ngẫu nhiêu (pseudorandom). Làm thế nào từ đoạn bit này ta xây dựng được đa thức đặc trưng của LFSR mà sinh ra tất cả các bit sau đó? Hơn nữa $l$ phải nhỏ nhất có thể.

Nhắc lại, đa thức đặc trưng là đa thức có dạng

\[P(x) = a_0 + a_1 x + \ldots + a_{n-1} x^{n-1} + a_n x^n\]

thì hàm boolean tuyến tính sinh ra bit tiếp theo sẽ có dạng

\[x_n = f(x_0, x_1, \ldots, x_{n-1}) = a_0 x_0 \oplus a_1 x_1 \oplus \ldots \oplus a_{n-1} x_{n-1}.\]

Tổng quát, công thức để sinh ra bit thứ $n+i$ sẽ là

\[x_{n+i} = f(x_i, x_{i+1}, \ldots, x_{n+i-1}) = a_0 x_i \oplus a_1 x_{i+1} \oplus \ldots \oplus a_{n-1} x_{n+i-1}\]

với $i = 0, 1, \ldots$

Thuật toán 4.1 (Thuật toán Berlekamp-Massey)

Đầu vào là dãy bit $u_0$, $u_1$, ..., $u_{l-1}$.

Đầu ra là đa thức đặc trưng bậc nhỏ nhất mà sinh ra toàn bộ dãy bit trên, bắt đầu từ các bit $u_0$, $u_1$, ... nhất định.

Bước -1. Gọi $n_0$ là vị trí đầu tiên mà $u_{n_0} = 1$ (các bit được đánh số từ $0$). Khi đó đặt $P_{-1}(x) = 1$ và $k_{-1} = 1$. Nếu $P_{-1}(x)$ sinh ra toàn bộ dãy bit thì ta dừng thuật toán. Ngược lại thì tiếp tục bước 1.

Bước 0. Đặt $P_0(x) = x^{n_0 + 1} \oplus P_{-1}(x)$ với $n_0$ là vị trí bit $1$ đầu tiên và đặt $k_0 = \deg P_0(x) = n_0 + 1$.

Ở mỗi bước từ đây trở đi, gọi $m$ là số sao cho

\[k_{-1} = k_0 = \ldots = k_{m-1} < k_{m} = k_{s+2} = \ldots\]

Bước $n$. Để tìm $P_n(x)$ ta tính $a = m - k_{m-1}$ và $b = n - k_{n-1}$.

Nếu $a \geqslant b$ thì

\[P_n(x) = P_{n-1}(x) \oplus x^{a-b} P_{m-1}(x).\]

Nếu $a < b$ thì

\[P_n(x) = x^{b-a} P_{n-1}(x) \oplus P_{m-1}.\]

Trong quá trình tìm $P_n(x)$, khi nào bậc $k_n$ của $P_n(x)$ thỏa mãn điều kiện số $m$ thì ta cập nhật lại số $m$.

Ở mỗi bước, nếu $P_n(x)$ sinh ra toàn bộ dãy bit thì ta dừng thuật toán.

Để xem cách hoạt động của thuật toán Berlekamp-Massey ta sẽ giải ví dụ sau.

Xét dãy bit $111100100$.

Đặt $n_0 = 0$, $P_{-1}(x) = 1$ và $k_{-1} = 0$.

Theo $P_{-1}(x) = 1$ thì $1 \to 1 \to 1 \to 1$, nghĩa là bit đầu thành bit thứ hai, bit thứ hai thành bit thứ ba và thứ ba thành thứ tư. Từ đó suy ra

\[P_0 (x) = P_1 (x) = P_2 (x) = P_3 (x) = x^{0+1} \oplus 1 = x \oplus 1.\]

Do $k_{-1} < k_0 = k_1 = k_2 = k_3$ ($0 < 1$) nên $m = 0$.

Để tìm $P_4(x)$, ta có $a = m- k_{m-1} = 0 - 0 = 0$ và $b = n - k_{n-1} = 4 - 1 = 3$. Do $a < b$ nên

\[P_4(x) = x^3 P_3(x) \oplus P_{-1}(x) = x^3 \cdot (x \oplus 1) \oplus 1 = x^4 \oplus x^3 \oplus 1.\]

Do $k_4 > k_3$ ($4 > 1$) nên $m = 4$.

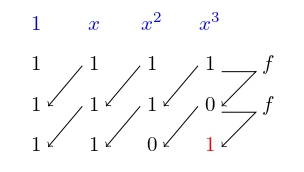
../../_images/berlekamp_massey-1.jpg — Hình 4.7 LFSR tương ứng $P_4(x)$¶

Trong hình trên, hàng đầu từ trái sang phải là $u_0, u_1, u_2, u_3$. Hàng thứ hai từ trái sang phải là $u_1, u_2, u_3, u_4$. Hàng thứ ba là $u_2, u_3, u_4, u_5$, nhưng $u_5 = 0$ theo dãy ban đầu nên LFSR sinh ra $1$ là chưa đúng, thuật toán chuyển sang bước tiếp theo.

Để tìm $P_5(x)$, ta có $a = m - k_{m-1} = 4 - 1 = 3$ và $b = n - k_{n-1} = 5 - 4 = 1$. Suy ra

\[P_5(x) = P_4(x) \oplus x^2 P_3 (x) = x^4 \oplus x^3 \oplus 1 \oplus x^2 \cdot (x \oplus 1) = x^4 \oplus x^2 \oplus 1.\]

Theo $P_5(x) = x^4 \oplus x^2 \oplus 1$ thì LFSR sẽ hoạt động như hình dưới đây. Cũng theo hình dưới thì $P_6(x) = P_5(x) = x^4 \oplus x^2 \oplus 1$.

../../_images/berlekamp_massey-2.jpg — Hình 4.8 LFSR tương ứng $P_5(x)$ và $P_6(x)$¶

Để tìm $P_7(x)$, ta có $a = m - k_{m-1} = 3$ và $b = n - k_{n-1} = 7 - 4 = 3$. Do $a \geqslant b$ nên

\[P_7(x) = P_6(x) \oplus P_3(x) = x^4 \oplus x^2 \oplus 1 \oplus x \oplus 1 = x^4 \oplus x^2 \oplus x.\]

Khi đó LFSR sẽ được sinh như hình.

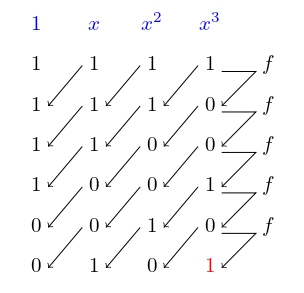
../../_images/berlekamp_massey-3.jpg — Hình 4.9 LFSR tương ứng $P_7(x)$¶

Để tìm $P_8(x)$, $a = 3$ và $b = 8 - 4 = 4$. Do $a < b$ nên

\[P_8(x) = x P_7(x) \oplus P_3(x) = x^5 \oplus x^3 \oplus x^2 \oplus x \oplus 1.\]

Lúc này LFSR sẽ là

../../_images/berlekamp_massey-4.jpg — Hình 4.10 LFSR tương ứng $P_8(x)$¶

Như vậy đa thức sinh ra dãy bit ban đầu là $x^5 \oplus x^3 \oplus x^2 \oplus x \oplus 1$. Thuật toán Berlekamp-Massey tìm ra đa thức đặc trưng với độ phức tạp là $8$ (tìm tới $P_8(x)$).

Ví dụ trên có thể được kiểm tra bởi chương trình Python ở đây.