3. Phương pháp chứng minh toán học

3.1. Chứng minh trực tiếp

Giả sử chúng ta có điều kiện ban đầu là \(P\) và ta cần chứng minh mệnh đề \(Q\).

Đối với chứng minh trực tiếp, từ \(P\) chúng ta suy ra \(P_1\) nào đó, rồi lại suy ra \(P_2\) từ \(P_1\). Chúng ta làm vậy cho đến khi nhận được mệnh đề \(Q\).

Chứng minh trực tiếp hữu dụng đối với những lời giải tuần tự từng bước.

Ví dụ 3.1

Cho tam giác \(ABC\) với \(G\), \(H\), \(O\) lần lượt là trọng tâm, trực tâm và tâm đường tròn ngoại tiếp tam giác \(ABC\). Chứng minh rằng ba điểm \(G\), \(H\) và \(O\) thẳng hàng.

Ở đây, với \(O\) là tâm đường tròn ngoại tiếp tam giác, ta vẽ đường tròn đó trước (Hình 3.1).

Tiếp theo, ta vẽ đường kính \(AD\).

Lúc này, vì góc \(\widehat{ACD}\) chắn nửa đường tròn (\(AD\) là đường kính) nên \(\widehat{ACD}\) là góc vuông, hay \(CD\) vuông góc \(AC\).

Tiếp theo, vì \(H\) là trực tâm nên \(BH\) vuông góc cạnh đối diện \(AC\).

Từ hai kết quả trên suy ra \(BH // CD\) vì cùng vuông góc \(AC\).

Tương tự ta cũng có \(CH // BD\).

Tứ giác \(BHCD\) có hai cặp cạnh song song là \(BH // CD\) và \(CH // BD\) nên \(BHCD\) là hình bình hành.

Giao điểm hai đường chéo của hình bình hành là trung điểm mỗi đường chéo. Gọi \(I_1\) là trung điểm \(BC\) thì \(I_1\) cũng là trung điểm \(HD\).

Vì \(O\) là trung điểm \(AD\), \(I_1\) là trung điểm \(HD\) nên \(OI_1\) là đường trung bình tam giác \(DHA\), hay \(\overrightarrow{OI_1} = \dfrac{1}{2}\overrightarrow{AH}\).

Do \(G\) là trọng tâm \(\triangle ABC\) và \(AI_1\) là trung tuyến (\(I_1\) là trung điểm \(BC\)) nên \(G\) chia đoạn thẳng \(AI_1\) theo tỉ lệ \(2:1\), nghĩa là \(\overrightarrow{AG} = 2\overrightarrow{GI_1}\).

Tiếp theo chúng ta biến đổi

\[\begin{split}\overrightarrow{AH} & = 2 \overrightarrow{OI_1} \\ \cancel{\overrightarrow{AG}} + \overrightarrow{GH} & = 2 (\overrightarrow{OG} + \overrightarrow{GI_1}) = 2\overrightarrow{OG} + \cancel{2\overrightarrow{GI_1}} \\ \overrightarrow{GH} & = 2\overrightarrow{OG}.\end{split}\]

Biểu thức cuối cùng chứng tỏ \(G\), \(H\) và \(O\) thẳng hàng, ngoài ra \(G\) chia đoạn thẳng \(HO\) theo tỉ lệ \(2:1\).

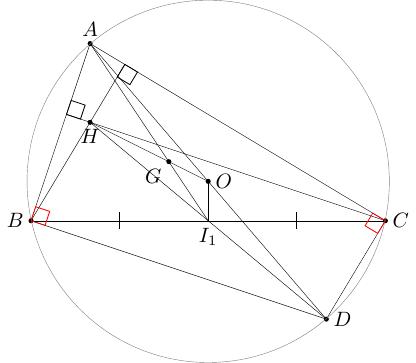
Hình 3.1 Đường thẳng Euler

3.2. Quy nạp toán học (cơ bản)

Giả sử ta muốn chứng minh một mệnh đề \(P\) đúng với mọi \(n \geqslant 1\). Phép quy nạp toán học hoạt động theo ba bước như sau:

1. Chứng minh mệnh đề \(P\) đúng với \(n=1\). Đây gọi là bước cơ sở.

2. Giả sử mệnh đề \(P\) đúng với \(n = k \geqslant 1\). Đây gọi là giả thiết quy nạp.

3. Chứng minh mệnh đề \(P\) đúng với \(n = k+1\) từ giả thiết quy nạp ở bước 2.

Như vậy phép quy nạp toán học (hay mathematical induction, математическая индукция) hoạt động theo bậc thang. Từ giả thiết quy nạp mệnh đề \(P\) đúng với \(n = 1\), theo chứng minh ở bước 3 thì mệnh đề \(P\) cũng đúng ở bước \(n = 1+1 = 2\). Do \(P\) đúng với \(n = 2\) nên cũng đúng ở \(n = 3\). Cứ tiếp tục như vậy \(P\) sẽ đúng với mọi \(n \geqslant 1\). Đây là sự hiệu quả đáng kinh ngạc của phép quy nạp toán học.

Ví dụ 3.2

Chứng minh công thức tổng quát cho tổng \(1 + 2 + \ldots + n`\) là \(\dfrac{n(n+1)}{2}\).

Với \(n = 1\) thì \(1 = \dfrac{1 (1 + 1)}{2}\). Như vậy công thức đúng cho \(n = 1\). Đây là bước cơ sở.

Giả sử mệnh đề đúng với \(n = k \geqslant 1\). Nghĩa là \(1 + 2 + \ldots + k = \dfrac{k(k+1)}{2}\). Đây là giả thiết quy nạp.

Bây giờ ta cần chứng minh mệnh đề đúng với \(n = k+1\), nghĩa là ta cần chứng minh

\[1 + 2 + \ldots + k + (k+1) = \dfrac{(k+1)(k+2)}{2}.\]

Từ giả thiết quy nạp ta suy ra

\[\begin{split}1 + 2 + \ldots + k + (k+1) = & \dfrac{k(k+1)}{2} + (k+1) \\ = & \dfrac{k(k+1) + 2(k+1)}{2} \\ = & \dfrac{(k+1)(k+2)}{2}.\end{split}\]

Vậy là ta đã có điều cần chứng minh, và công thức đã được chứng minh đúng với mọi \(n \geqslant 1\).

Nhận xét 3.1

Tùy thuộc bài toán, bước cơ sở có thể không phải bắt đầu từ \(1\) mà là một số nguyên dương nào đó khác.

3.3. Quy nạp toán học (mạnh)

Quy nạp toán học mạnh (strong induction) là một phiên bản mạnh hơn của phép quy nạp toán học ở trên.

Trong phép quy nạp toán học mạnh, giả thiết quy nạp sẽ được thay bằng: Giả sử mệnh đề \(P\) ĐÚNG TỚI \(n = k \geqslant 1\).

Điểm khác biệt của quy nạp mạnh với quy nạp ban đầu là việc giả thiết quy nạp đúng với mọi \(n\) nhỏ hơn hoặc bằng \(k\) và chúng ta sẽ chứng minh mệnh đề đúng với \(n = k + 1\). Trong khi đó ở quy nạp ban đầu thì giả thiết quy nạp chỉ đúng với \(n = k\) thôi.

Tính đúng đắn của quy nạp mạnh vẫn giống như quy nạp thông thường, nghĩa là vẫn hoạt động theo bậc thang. Khi mệnh đề đúng với \(n = 1\) (bước cơ sở) thì chứng minh ở bước 3 cho kết quả mệnh đề \(P\) đúng với \(n = 2\). Do mệnh đề \(P\) đúng với \(n = 1, 2\) nên sẽ đúng với \(n = 3\). Cứ tiếp tục như vậy thì \(P\) sẽ đúng với mọi \(n \geqslant 1\).

Tại sao chúng ta cần dùng quy nạp toán học mạnh khi bản chất vẫn giống quy nạp thông thường?

Lý do là đôi khi chúng ta chứng minh \(n = k + 1\) không dựa trên \(n = k\), mà là một điểm nào đó nhỏ hơn, nghĩa là trong khoảng \([1, k]\).

Ví dụ 3.3

Dãy số Fibonacci định nghĩa bởi \(F_1 = F_2 = 1\) và \(F_{n+2} = F_{n+1} + F_n\) với mọi \(n \geqslant 1\). Chứng minh rằng công thức tổng quát của dãy Fibonacci là

\[F_n = \frac{1}{\sqrt{5}} \left[ \left(\frac{1 + \sqrt{5}}{2}\right)^n - \left(\frac{1 - \sqrt{5}}{2}\right)^n \right].\]

Khi \(n = 1\) thì ta có \(F_1 = 1\), đúng với điều kiện ban đầu.

Khi \(n = 2\) thì ta có \(F_2 = 1\), đúng với điều kiện ban đầu.

Giả thiết quy nạp: giả sử với mọi \(n = k \geqslant 1\) ta đều có \(F_k = \dfrac{1}{\sqrt{5}} \left[ \left(\dfrac{1 + \sqrt{5}}{2}\right)^k - \left(\dfrac{1 - \sqrt{5}}{2}\right)^k \right]\).

Khi đó, với \(n = k+1\), ta có

\[\begin{split}F_{k+1} & = F_{k} + F_{k-1} \\ & = \dfrac{1}{\sqrt{5}} \left[ \left(\dfrac{1 + \sqrt{5}}{2}\right)^k - \left(\dfrac{1 - \sqrt{5}}{2}\right)^k \right] + \dfrac{1}{\sqrt{5}} \left[ \left(\dfrac{1 + \sqrt{5}}{2}\right)^{k-1} - \left(\dfrac{1 - \sqrt{5}}{2}\right)^{k-1} \right] \\ & = \dfrac{1}{\sqrt{5}} \left[ \left(\dfrac{1 + \sqrt{5}}{2}\right)^k + \left(\dfrac{1 + \sqrt{5}}{2}\right)^{k-1} \right] - \dfrac{1}{\sqrt{5}} \left[ \left(\dfrac{1 - \sqrt{5}}{2}\right)^k + \left(\dfrac{1 - \sqrt{5}}{2}\right)^{k-1} \right] \\ & = \dfrac{1}{\sqrt{5}} \left(\dfrac{1 + \sqrt{5}}{2}\right)^{k-1} \left(\dfrac{1 + \sqrt{5}}{2} + 1\right) - \dfrac{1}{\sqrt{5}} \left(\dfrac{1 - \sqrt{5}}{2}\right)^{k-1} \left(\dfrac{1 - \sqrt{5}}{2} + 1\right).\end{split}\]

Để ý rằng

\[\begin{split}\dfrac{1 + \sqrt{5}}{2} + 1 & = \dfrac{3 + \sqrt{5}}{2} = \dfrac{6 + 2\sqrt{5}}{4} = \dfrac{1 + 2\sqrt{5} + \left(\sqrt{5}\right)^2}{4} \\ & = \dfrac{\left(1 + \sqrt{5}\right)^2}{2^2} = \left(\dfrac{1 + \sqrt{5}}{2}\right)^2,\end{split}\]

tương tự ta cũng có \(\dfrac{1 - \sqrt{5}}{2} + 1 = \left(\dfrac{1 - \sqrt{5}}{2}\right)^2\), nên ở trên suy ra

\[\begin{split}F_{k+1} & = \dfrac{1}{\sqrt{5}} \left(\dfrac{1 + \sqrt{5}}{2}\right)^{k-1} \left(\dfrac{1 + \sqrt{5}}{2}\right)^2 + \dfrac{1}{\sqrt{5}} \left(\dfrac{1 - \sqrt{5}}{2}\right)^{k-1} \left(\dfrac{1 - \sqrt{5}}{2}\right)^2 \\ & = \dfrac{1}{\sqrt{5}} \left[ \left(\dfrac{1 + \sqrt{5}}{2}\right)^{k+1} - \left(\dfrac{1 - \sqrt{5}}{2}\right)^{k+1} \right].\end{split}\]

Như vậy mệnh đề đúng với \(n = k+1\) và ta có điều phải chứng minh.

Ở đây quy nạp mạnh thể hiện ở việc ta cần giả thiết đúng với \(n = k\) và \(n = k-1\) để chứng minh cho \(n = k+1\).

3.4. Chứng minh bằng phản chứng

Giả sử chúng ta có điều kiện \(P\) và cần chứng minh kết quả \(Q\). Điều này tương đương với mệnh đề logic \(P \Rightarrow Q\). Chứng minh bằng phản chứng dựa trên sự tương đương của các mệnh đề logic, nghĩa là

\[(P \Rightarrow Q) \Longleftrightarrow (\bar{Q} \Rightarrow \bar{P}).\]

Khi đó, từ kết quả \(Q\) cần chứng minh, chúng ta giả sử rằng đang có \(\bar{Q}\), tức là phủ định của mệnh đề cần chứng minh. Bằng các lập luận logic chúng ta sẽ suy ra được điều trái với điều kiện ban đầu, tức là \(\bar{P}\). Đây là cơ sở của phép chứng minh bằng phản chứng.

Ví dụ 3.4

Chứng minh rằng với mọi số tự nhiên \(n\), nếu \(n^3\) chia hết cho \(3\) thì \(n\) chia hết cho \(3\).

Ở đây:

1. Điều kiện, tức mệnh đề \(P\), là "\(n^3\) chia hết cho \(3\)".

2. Mệnh đề cần chứng minh \(Q\) là "\(n\) chia hết cho \(3\)".

Ta suy ra:

1. Phủ định của mệnh đề \(P\) là "\(n^3\) không chia hết cho \(3\)", tức mệnh đề \(\bar{P}\).

2. Phủ định của mệnh đề \(Q\) là "\(n\) không chia hết cho \(3\)", tức mệnh đề \(\bar{Q}\).

Như vậy phép phản chứng đưa ta tới việc chứng minh: nếu số tự nhiên \(n\) không chia hết cho \(3\) thì \(n^3\) không chia hết cho \(3\).

Nếu \(n\) không chia hết cho \(3\) thì \(n\) có dạng \(3k+1\) hoặc \(3k+2\) với \(k \in \mathbb{Z}\).

• nếu \(n = 3k+1\) thì \(n^3 = 27k^3 + 27k^2 + 9k + 1\), khi chia \(3\) sẽ dư \(1\). Khi đó \(n^3\) không chia hết cho \(3\);

• nếu \(n = 3k+2\) thì \(n^3 = 27k^3 + 54k^2 + 36k + 8\), khi chia \(3\) sẽ dư \(2\) (vì \(8\) chia \(3\) dư \(2\)). Khi đó \(n^3\) cũng không chia hết cho \(3\).

Như vậy khi \(n\) không chia hết cho \(3\) (mệnh đề \(\bar{Q}\)) thì \(n^3\) cũng không chia hết cho \(3\) (mệnh đề \(\bar{P}\)). Theo phản chứng ta có, nếu \(n^3\) chia hết cho \(3\) (mệnh đề \(P\)) thì \(n\) chia hết cho \(3\) (mệnh đề \(Q\)). Đây là điều phải chứng minh.