6.1. Extension Fields

6.1.1. Extension Fields

Định nghĩa 6.1 (Mở rộng trường)

Trường \(E\) được gọi là mở rộng trường (hay extension field) của trường \(F\) nếu \(F\) là trường con của \(E\). Khi đó \(F\) được gọi là trường cơ sở (hay base field) và kí hiệu \(F \subset E\).

Ví dụ 6.1

Trường nào nhỏ nhất chứa \(\mathbb{Q}\) và \(\sqrt{2}\)?

Đáp án là trường

\[\mathbb{Q}(\sqrt{2}) = \{ a + b \sqrt{2} : a, b \in \mathbb{Q} \}.\]

Việc chứng minh \(\mathbb{Q}(\sqrt{2})\) là trường khá đơn giản, phần tử nghịch đảo đối với phép nhân của \(a + b \sqrt{2}\) là

\[\frac{a}{a^2 - 2 b^2} + \frac{-2b}{a^2 - 2 b^2} \sqrt{2}.\]

Ví dụ 6.2

Trường nào nhỏ nhất chứa \(\mathbb{Q}\) và \(i\) (ở đây \(i\) là đơn vị ảo, \(i^2 = -1\))?

Đáp án là trường

\[\mathbb{Q}(i) = \{ a + b i : a, b \in \mathbb{Q} \}.\]

Tương tự, ở đây phần tử nghịch đảo đối với phép nhân của \(a + b i\) là

\[\frac{a}{a^2 + b^2} + \frac{-b}{a^2 + b^2} i.\]

Ở đây \(\mathbb{Q}(\sqrt{2})\) và \(\mathbb{Q}(i)\) đều là mở rộng của \(\mathbb{Q}\) và đều là tập con của \(\mathbb{C}\). Tuy nhiên hai trường này không phải tập con của nhau.

Như vậy, bằng việc mở rộng \(\mathbb{Q}\) với \(\sqrt{2}\) ta có trường \(\mathbb{Q}(\sqrt{2})\).

Tương tự, bằng việc mở rộng \(\mathbb{Q}\) với \(i\) ta có trường \(\mathbb{Q}(i)\).

Vậy trường nào chứa \(\mathbb{Q}\), \(\sqrt{2}\) và \(i\)?

Ví dụ 6.3

Trường chứa cả \(\mathbb{Q}\), \(\sqrt{2}\) và \(i\) là tập hợp

\[\mathbb{Q}(\sqrt{2}, i) = \{ a + b\sqrt{2} + c i + d \sqrt{2} i : a, b, c, d \in \mathbb{Q} \}.\]

Trường trên có thể suy ra từ logic sau. Ta đã có \(\mathbb{Q}(i)\) chứa \(\mathbb{Q}\) và \(i\). Ta muốn thêm \(\sqrt{2}\) vào trường \(\mathbb{Q}(i)\) nên ta sẽ muốn mở rộng \(\mathbb{Q}(i)\) lên \(\mathbb{Q}(i)(\sqrt{2})\).

Khi đó \(\mathbb{Q}(i)(\sqrt{2})\) tương tự sẽ có dạng

\[\mathbb{Q}(i)(\sqrt{2}) = \{ \alpha + \beta \sqrt{2} : \alpha, \beta \in \mathbb{Q}(i) \}.\]

Nói cách khác \(\alpha = a + b i\) và \(\beta = c + d i\), \(a, b, c, d \in \mathbb{Q}\), nên ta có

\[\alpha + \beta \sqrt{2} = a + b i + c \sqrt{2} + d \sqrt{2} i, \quad a, b, c, d \in \mathbb{Q}.\]

Khi đó ta viết

\[\mathbb{Q}(i)(\sqrt{2}) = \mathbb{Q}(\sqrt{2}, i) = \{ a + b\sqrt{2} + c i + d \sqrt{2} i : a, b, c, d \in \mathbb{Q} \}.\]

Nhận xét 6.1

1. \(\mathbb{Q}(\sqrt{2})\) là trường con của \(\mathbb{R}\) nhưng \(\mathbb{Q}(i)\) không phải.

2. \(\mathbb{Q}(i)\) nhỏ hơn \(\mathbb{C}\) rất nhiều (không chứa \(\sqrt{2}\)).

3. \(\mathbb{Q}(\sqrt{2})\) chứa tất cả nghiệm của đa thức \(f(x) = x^2 - 2\) trên \(\mathbb{Q}\). Do đó \(\mathbb{Q}(\sqrt{2})\) được gọi là trường phân rã của đa thức \(f(x)\).

6.1.2. Biểu diễn quan hệ giữa các trường qua lattice

Ở phần trước, \(\mathbb{Q}(\sqrt{2})\) là mở rộng của \(\mathbb{Q}\) và với hai phần tử \(a, b \in \mathbb{Q}\) xác định một phần tử \(a + b \sqrt{2} \in \mathbb{Q}(\sqrt{2})\).

Do \(a + b \sqrt{2} = a \cdot 1 + b \cdot \sqrt{2}\) nên \(\{ 1, \sqrt{2} \}\) là cơ sở (hay basis) của \(\mathbb{Q}(\sqrt{2})\). Cơ sở chứa hai phần tử nên ta nói bậc của mở rộng đơn (hay degree) từ \(\mathbb{Q}\) lên \(\mathbb{Q}(\sqrt{2})\) là \(2\).

Tương tự, mở rộng từ \(\mathbb{Q}\) lên \(\mathbb{Q}(i)\) cũng có bậc là \(2\) với cơ sở là \(\{ 1, i \}\).

Ta kí hiệu bậc của mở rộng đơn là

\[\boxed{[E : F].}\]

Như vậy ta cũng các trường \(\mathbb{Q}(\sqrt{2})\), \(\mathbb{Q}(\sqrt{3})\) và \(\mathbb{Q}(\sqrt{6})\) là các mở rộng đơn bậc \(2\) của \(\mathbb{Q}\) (Hình 6.1).

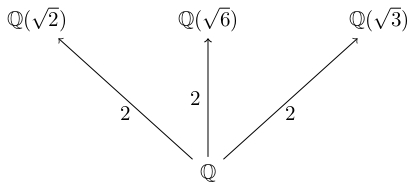
Hình 6.1 Mở rộng trường \(\mathbb{Q}\) lên \(\mathbb{Q}(\sqrt{2})\), \(\mathbb{Q}(\sqrt{3})\) và \(\mathbb{Q}(\sqrt{6})\)

Do \(\sqrt{6} = \sqrt{2} \cdot \sqrt{3}\) dẫn ta tới câu hỏi, trường nào nhỏ nhất chứa cả \(\sqrt{2}\) và \(\sqrt{3}\)?

Thực hiện tương tự với \(\mathbb{Q}(\sqrt{2}, i)\) ở trên ta có trường

\[\mathbb{Q}(\sqrt{2}, \sqrt{3}) = \mathbb{Q}(\sqrt{2})(\sqrt{3}) = \{ a + b \sqrt{2} + c \sqrt{3} + d \sqrt{6} : a, b, c, d \in \mathbb{Q} \}\]

là trường nhỏ nhất chứa cả \(\sqrt{2}\) và \(\sqrt{3}\).

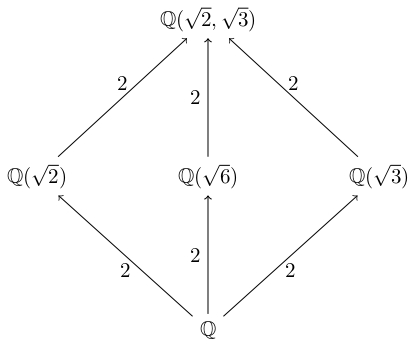
Ở đây, \(\mathbb{Q}(\sqrt{2}, \sqrt{3})\) là mở rộng bậc \(4\) của \(\mathbb{Q}\) với cơ sở là \(\{ 1, \sqrt{2}, \sqrt{3}, \sqrt{6} \}\).

Bằng việc mở rộng từ \(\mathbb{Q}(\sqrt{2})\) lên \(\mathbb{Q}(\sqrt{2}, \sqrt{3}) = \mathbb{Q}(\sqrt{2})(\sqrt{3})\) ta cũng có đây là mở rộng bậc \(2\) (tương tự chứng minh phía trên cho \(\mathbb{Q}(\sqrt{2}, i)\)). Như vậy mở rộng từ \(\mathbb{Q}(\sqrt{3})\) lên \(\mathbb{Q}(\sqrt{2}, \sqrt{3})\) cũng là mở rộng bậc \(2\).

Vậy mở rộng từ \(\mathbb{Q}(\sqrt{6})\) lên \(\mathbb{Q}(\sqrt{2}, \sqrt{3})\) là bậc mấy? Để xác định ta cần chứng minh nhận xét sau

Nhận xét 6.2

\(\mathbb{Q}(\sqrt{2}, \sqrt{3}) \equiv \mathbb{Q}(\sqrt{2} + \sqrt{3})\), trong đó \(\mathbb{Q}(\sqrt{2} + \sqrt{3})\) là trường nhỏ nhất chứa \(\mathbb{Q}\) và \(\sqrt{2} + \sqrt{3}\).

Chứng minh

Ta chứng minh \(\mathbb{Q}(\sqrt{2}, \sqrt{3}) \subset \mathbb{Q}(\sqrt{2} + \sqrt{3})\).

Do \(\sqrt{2} + \sqrt{3}\) nên nghịch đảo \(\dfrac{1}{\sqrt{2} + \sqrt{3}} = \sqrt{3} - \sqrt{2} \in \mathbb{Q}(\sqrt{2} + \sqrt{3})\).

Khi đó, \(\dfrac{1}{2} \cdot (\sqrt{2} + \sqrt{3}) \pm \dfrac{1}{2} \cdot (\sqrt{3} - \sqrt{2}) \in \mathbb{Q}(\sqrt{2} + \sqrt{3})\).

Vế trái sẽ bằng \(\sqrt{2}\) hoặc \(\sqrt{3}\). Như vậy \(\sqrt{2}, \sqrt{3} \in \mathbb{Q}(\sqrt{2} + \sqrt{3})\).

Phép nhân trên trường cho ta \(\sqrt{2} \cdot \sqrt{3} = \sqrt{6} \in \mathbb{Q}(\sqrt{2} + \sqrt{3})\).

Như vậy với mọi \(a, b, c, d \in \mathbb{Q}\) ta có \(a + b \sqrt{2} + c \sqrt{3} + d \sqrt{6} \in \mathbb{Q}(\sqrt{2} + \sqrt{3})\). Điều này tương đương với \(\mathbb{Q}(\sqrt{2}, \sqrt{3}) \subset \mathbb{Q}(\sqrt{2} + \sqrt{3})\).

Nhưng mà \(\mathbb{Q}(\sqrt{2} + \sqrt{3})\) là trường nhỏ nhất chứa \(\mathbb{Q}\) và \(\sqrt{2} + \sqrt{3}\), và \(\mathbb{Q}(\sqrt{2}, \sqrt{3})\) là trường nhỏ nhất chứa \(\sqrt{2}\) và \(\sqrt{3}\), kéo theo chứa cả \(\sqrt{2} + \sqrt{3}\) nên \(\mathbb{Q}(\sqrt{2} + \sqrt{3}) \equiv \mathbb{Q}(\sqrt{2}, \sqrt{3})\).

Ta có \(\mathbb{Q}(\sqrt{6}) = \{ a + b \sqrt{6} : a, b \in \mathbb{Q} \}\). Khi đó

(6.1)\[\mathbb{Q}(\sqrt{6})(\sqrt{2} + \sqrt{3}) = \{ \alpha + \beta (\sqrt{2} + \sqrt{3}) : \alpha, \beta \in \mathbb{Q}(\sqrt{6}) \}.\]

Đặt \(\alpha = a + b \sqrt{6}\) và \(\beta = c + d \sqrt{6}\), như vậy mỗi phần tử trong \(\mathbb{Q}(\sqrt{6})(\sqrt{2} + \sqrt{3})\) có dạng

\[\begin{split}a + b \sqrt{6} + (c + \sqrt{6})(\sqrt{2} + \sqrt{3}) = & a + (c + 3d) \sqrt{2} + (c + 2d) \sqrt{3} + b \sqrt{6} \\ = & a' + b' \sqrt{2} + c' \sqrt{3} + d' \sqrt{6},\end{split}\]

với \(a \to a'\), \(c+3d \to b'\), \(c + 2d \to c'\) và \(b \to d'\).

Biến đổi này tương đương với hệ phương trình tuyến tính

\[\begin{split}\begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 3 \\ 0 & 0 & 1 & 2 \\ 0 & 1 & 0 & 0 \end{pmatrix} \begin{pmatrix} a \\ b \\ c \\ d \end{pmatrix} = \begin{pmatrix} a' \\ b' \\ c' \\ d' \end{pmatrix}\end{split}\]

Ma trận trên khả nghịch trên \(\mathbb{Q}\), do đó \(\mathbb{Q}(\sqrt{6})(\sqrt{2} + \sqrt{3}) \equiv \mathbb{Q}(\sqrt{2}, \sqrt{3})\). Ở dạng biểu diễn (6.1) ta suy ra mở rộng từ \(\mathbb{Q}(\sqrt{6})\) lên \(\mathbb{Q}(\sqrt{2}, \sqrt{3})\) là mở rộng bậc \(2\).

Sơ đồ mở rộng trường bây giờ như sau

6.1.3. Splitting Field

Định nghĩa 6.2 (Trường phân rã)

Xét trường \(F\) và đa thức khác hằng

\[p(x) = a_n x^n + a_{n-1} x^{n-1} + \ldots + a_1 x + a_0\]

trên \(F[x]\), ở đây \(a_i \in F\) với mọi \(i = 1, 2, \ldots\)

Trường mở rộng \(E\) của trường \(F\) được gọi là trường phân rã (hay splitting field) của \(p(x)\) nếu tồn tại các phần tử \(\alpha_1\), \(\alpha_2\), ..., \(\alpha_n\) thuộc \(E\) sao cho \(E = F(\alpha_1, \alpha_2, \ldots, \alpha_n)\) và

\[p(x) = (x - \alpha_1) (x - \alpha_2) \cdots (x - \alpha_n).\]

Khi đó ta nói đa thức \(p(x) \in F[x]\) phân rã (split) trong \(E\) nếu nó phân tích thành các nhân tử bậc nhất (tuyến tính) trong \(E[x]\).

Nói nôm na, nếu đa thức có hệ số trong một trường \(F\) nào đó (tức thuộc \(F[x]\)) thì các nghiệm của nó nằm trong một trường lớn hơn chứa \(F\).

Ví dụ 6.4

Đa thức \(f(x) = x^2 - 2\) trên \(\mathbb{Q}[x]\) không có nghiệm trên \(\mathbb{Q}\). Tuy nhiên \(\mathbb{Q}(\sqrt{2})\) là trường chứa \(\mathbb{Q}\) và các nghiệm của \(f(x)\) là \(\pm \sqrt{2}\). Vì vậy \(\mathbb{Q}(\sqrt{2})\) là trường phân rã của \(f(x)\).

Ví dụ 6.5

Đa thức \(g(x) = x^2 + 1\) trên \(\mathbb{Q}[x]\) không có nghiệm trên \(\mathbb{Q}\). Tuy nhiên \(g(x)\) có hai nghiệm là \(\pm i\) và \(\mathbb{Q}(i)\) chứa cả \(\mathbb{Q}\) và \(\pm i\) nên \(\mathbb{Q}(i)\) là một trường phân rã của \(g(x)\).

Ở đây, bậc của đa thức \(f(x) = x^2 - 2\) bằng với bậc của mở rộng trường từ \(\mathbb{Q}\) lên \(\mathbb{Q}(\sqrt{2})\).

Tương tự, bậc của mở rộng trường từ \(\mathbb{Q}\) lên \(\mathbb{Q}(\sqrt{3})\) bằng bậc đa thức \(g(x) = x^2 - 3\), và bậc của mở rộng trường từ \(\mathbb{Q}\) lên \(\mathbb{Q}(\sqrt{6})\) bằng với bậc đa thức \(h(x) = x^2 - 6\).

Ở trên ta đã chứng minh bậc của mở rộng trường từ \(\mathbb{Q}(\sqrt{2})\) lên \(\mathbb{Q}(\sqrt{2}, \sqrt{3})\) là \(2\), điều này tương ứng với bậc của đa thức

\[k(x) = (x^2 - 2)(x^2 - 3) = x^4 - 5 x + 6.\]

Tổng kết lại, nếu \(E\) là trường phân rã của \(F\) trên đa thức \(f(x) \in F[x]\) thì bậc của mở rộng trường từ \(F\) lên \(E\) bằng với bậc của \(f(x)\).

Từ sơ đồ mở rộng trường bên trên ta có sơ đồ với đa thức tương ứng.

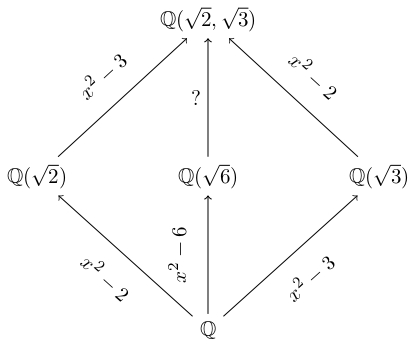
Vậy còn mở rộng từ \(\mathbb{Q}(\sqrt{6})\) thành \(\mathbb{Q}(\sqrt{2}, \sqrt{3})\)? Ở trên ta đã chứng minh rằng đây là mở rộng bậc \(2\). Vậy chúng ta cần tìm một đa thức bậc \(2\) có hệ số trong \(\mathbb{Q}(\sqrt{6})\) mà không có nghiệm trong \(\mathbb{Q}(\sqrt{6})\).

Quay lại một chút, ta đã mở rộng \(\mathbb{Q}(\sqrt{6})\) lên \(\mathbb{Q}(\sqrt{2}, \sqrt{3})\) với sự trợ giúp của phần tử \(\sqrt{2} + \sqrt{3}\). Từ đây ta có thể xây dựng đa thức

\[m(x) = x^2 - (\sqrt{2} + \sqrt{3})^2 = x^2 - 5 - 2 \sqrt{6}.\]

Đa thức \(m(x)\) có hệ số trong \(\mathbb{Q}(\sqrt{6})\) nhưng không có nghiệm trong \(\mathbb{Q}(\sqrt{6})\), mà trong \(\mathbb{Q}(\sqrt{2}, \sqrt{3})\). Ta có điều phải chứng minh.

6.1.4. Field automorphism

Nhận xét 6.3

Tập hợp tất cả tự đẳng cấu (automorphism) trên trường \(F\) là nhóm với toán tử là hợp của các hàm. Kí hiệu là \(Aut(F)\).

Chứng minh

Dễ thấy nếu \(\sigma\) và \(\tau\) là tự đẳng cấu trên \(F\) thì \(\sigma \tau\) và \(\sigma^{-1}\) cũng là tự đẳng cấu trên \(F\) (đều là song ánh). Ánh xạ đồng nhất hiển nhiên là tự đẳng cấu nên sẽ là phần tử đơn vị của nhóm.

Nhận xét 6.4

Gọi \(E\) là mở rộng trường của \(F\). Khi đó tập hợp tất cả tự đẳng cấu trên \(E\) mà cố định phần tử của \(F\) tạo thành một nhóm, nghĩa là tập hợp tất cả các tự đẳng cấu \(\sigma : E \to E\) sao cho \(\sigma(\alpha) = \alpha\) với mọi \(\alpha \in F\) tạo thành một nhóm.

Chứng minh

Từ nhận xét ở trên thì tập hợp tất cả tự đẳng cấu trên \(E\) tạo thành một nhóm \(Aut(E)\). Như vậy để chứng minh nhận xét này thì chúng ta chỉ cần chỉ ra tập hợp tất cả tự đẳng cấu của \(E\) mà cố định phần tử trong \(F\) là một nhóm con của \(Aut(E)\).

Gọi \(\sigma\) và \(\tau\) là hai tự đẳng cấu của \(E\) sao cho \(\sigma(\alpha) = \alpha\) và \(\tau(\alpha) = \alpha\) với mọi \(\alpha \in F\).

Khi đó \(\sigma(\tau(\alpha)) = \sigma(\alpha) = \alpha\) nên ánh xạ hợp \(\sigma \tau\) cũng nằm trong tập các tự đẳng cấu trên \(E\) mà cố định phần tử trên \(F\).

Ngoài ra, \(\sigma^{-1}(\alpha) = \alpha\) và ánh xạ đồng nhất cố định mọi phần tử trên \(E\). Như vậy tập tất cả tự đẳng cấu trên \(E\) mà cố định mọi phần tử trong \(F\) là nhóm con của \(Aut(E)\).

Ở trên ta kí hiệu nhóm tất cả các tự đẳng cấu trên \(E\) là \(Aut(E)\). Bây giờ ta sẽ định nghĩa nhóm Galois.

Định nghĩa 6.3 (Nhóm Galois)

Gọi \(E\) là mở rộng trường của \(F\). Ta nói nhóm Galois (hay Galois group) của \(E\) trên \(F\) là nhóm tất cả tự đẳng cấu của \(E\) mà cố định phần tử trên \(F\), nghĩa là

\[G(E / F) = \{ \sigma \in Aut(E) : \sigma(\alpha) = \alpha \ \text{với mọi} \ \sigma \in F \}.\]

Nếu \(f(x)\) là đa thức trong \(F[x]\) và \(E\) là trường phân rã của \(f(x)\) theo \(F\) thì ta định nghĩa nhóm Galois của \(f(x)\) theo \(G(E / F)\).

Ví dụ 6.6

Liên hợp của số phức xác định bởi ánh xạ quen thuộc

\[\sigma : a + bi \to a - bi\]

là một tự đẳng cấu trên tập các số phức \(\mathbb{C}\). Vì \(\mathbb{R} \subset \mathbb{C}\) và

\[\sigma(a) = \sigma(a + 0i) = a - 0i = a\]

nên ánh xạ \(\sigma\) thuộc \(G(\mathbb{C} / \mathbb{R})\).

Ví dụ 6.7

Xét các trường \(\mathbb{Q} \subset \mathbb{Q}(\sqrt{5}) \subset \mathbb{Q}(\sqrt{3}, \sqrt{5})\). Khi đó với \(a, b \in \mathbb{Q}(\sqrt{5})\) thì ánh xạ

\[\sigma(a + b\sqrt{3}) = a - b\sqrt{3}\]

là tự đẳng cấu trên \(\mathbb{Q}(\sqrt{3}, \sqrt{5})\) mà cố định \(\mathbb{Q}(\sqrt{5})\).

Thật vậy, giả sử \(a = s + t \sqrt{5}\) và \(b = u + v \sqrt{5}\) với \(s, t, u, v \in \mathbb{Q}\). Khi đó

\[\sigma(a + b\sqrt{3}) = a - b\sqrt{3} = s + t\sqrt{5} - (u + v\sqrt{5}) \sqrt{3} = (s - u\sqrt{3}) + (t - v\sqrt{3}) \sqrt{5}.\]

Ta có

\[a + b\sqrt{3} = (s + u\sqrt{3}) + (t + v\sqrt{3}) \sqrt{5} \in \mathbb{Q}(\sqrt{5})\]

khi và chỉ khi \(s + u\sqrt{3} \in \mathbb{Q}\) và \(t + v\sqrt{3} \in \mathbb{Q}\). Nói cách khác \(u = v = 0\). Như vậy

\[\sigma(a + b\sqrt{3}) = \sigma(s + t\sqrt{5}) = s + t\sqrt{5}.\]

Phần tử \(s + t\sqrt{5} \in \mathbb{Q}(\sqrt{5})\) nên \(\sigma\) cố định các phần tử trên \(\mathbb{Q}(\sqrt{5})\).

Tương tự ta cũng có ánh xạ

\[\tau(a + b\sqrt{5}) = a - b\sqrt{5}\]

là tự đẳng cấu trên \(\mathbb{Q}(\sqrt{3}, \sqrt{5})\) mà cố định \(\mathbb{Q}(\sqrt{3})\).

Tuy nhiên ánh xạ hợp \(\mu = \sigma \tau\) không cố định cả \(\mathbb{Q}(\sqrt{3})\) lẫn \(\mathbb{Q}(\sqrt{5})\).

Chúng ta cũng chứng minh được rằng \(\{ id, \sigma, \tau, \mu \}\) là nhóm Galois của \(\mathbb{Q}(\sqrt{3}, \sqrt{5})\) trên \(\mathbb{Q}\) vì các ánh xạ đó cố định phần tử thuộc \(\mathbb{Q}\) (không chứa căn).

Như vậy nhóm Galois của \(\mathbb{Q}(\sqrt{3}, \sqrt{5})\) có \(4\) phần tử, tức là \(\lvert G(\mathbb{Q}(\sqrt{3}, \sqrt{5}) / \mathbb{Q}) \rvert = 4\). Ở trên phần trường phân rã mình cũng đã chỉ ra rằng \([ \mathbb{Q}(\sqrt{3}, \sqrt{5}) : \mathbb{Q} ] = 4\) nên ở đây

\[\lvert G(\mathbb{Q}(\sqrt{3}, \sqrt{5}) / \mathbb{Q}) \rvert = [\mathbb{Q}(\sqrt{3}, \sqrt{5}) : \mathbb{Q}] = 4.\]

Một điều nữa là trường \(\mathbb{Q}(\sqrt{3}, \sqrt{5})\) cũng chính là không gian vector trên \(\mathbb{Q}\) với cơ sở là tập \(\{ 1, \sqrt{3}, \sqrt{5}, \sqrt{15} \}\). Tập này cũng có \(4\) phần tử.

Một câu hỏi tự nhiên được đặt ra ở đây: việc số lượng phần tử của các tập hợp ở đây bằng nhau là ngẫu nhiên hay có lý do?

Nhận xét 6.5

Cho \(E\) là một mở rộng trường của \(F\) và \(f(x)\) là đa thức trên \(F[x]\). Khi đó mỗi tự đẳng cấu trong \(G(E / F)\) xác định một hoán vị các nghiệm của \(f(x)\) trên \(E\).

Chứng minh

Đặt

\[f(x) = a_0 + a_1 x + a_2 x^2 + \cdots + a_n x^n\]

và giả sử \(\alpha \in E\) là một nghiệm của \(f(x)\). Khi đó với tự đẳng cấu \(\sigma \in G(E/F)\) ta có

\[\begin{split}0 & = \sigma(0) \\ & = \sigma(f(\alpha)) \\ & = \sigma(a_0 + a_1 \alpha + a_2 \alpha^2 + \cdots + a_n \alpha^n) \\ & = \sigma(a_0) + \sigma(a_1 \alpha) + \sigma(a_2 \alpha^2) + \cdots + \sigma(a_n \alpha^n) \\ & = \sigma(a_0) + \sigma(a_1) \sigma(\alpha) + \sigma(a_2) \sigma(\alpha^2) + \cdots + \sigma(a_n) \sigma(\alpha^n).\end{split}\]

Trong đó hai dòng cuối là từ định nghĩa của tự đẳng cấu. Thêm nữa \(\sigma(\alpha^k) = \sigma(\alpha)^k\) và do \(\sigma \in G(E/F)\) nên \(\sigma(a_i) = a_i\) với mọi \(0 \leqslant i \leqslant n\). Như vậy có thể suy ra

\[0 = a_0 + a_1 \sigma(\alpha) + a_2 \sigma(\alpha)^2 + \cdots + a_n \sigma(\alpha)^n,\]

nói cách khác \(\sigma(\alpha)\) cũng là nghiệm của \(f(x)\).

Cho \(E\) là mở rộng trường của trường \(F\). Hai phần tử \(\alpha, \beta \in E\) được gọi là liên hợp trên \(F\) nếu chúng có cùng đa thức tối tiểu. Ở đây, đa thức tối tiểu được hiểu là đa thức có bậc nhỏ nhất nhận \(\alpha\) và \(\beta\) làm nghiệm.

Ví dụ, trên trường \(\mathbb{Q}(\sqrt{2})\) thì hai phần tử \(\sqrt{2}\) và \(-\sqrt{2}\) là liên hợp trên \(\mathbb{Q}\) vì chúng đều là nghiệm của đa thức tối giản \(x^2 - 2\).

Nhận xét 6.6

Nếu \(\alpha\) và \(\beta\) liên hợp trên \(F\) thì tồn tại đẳng cấu \(\sigma : F(\alpha) \to F(\beta)\) sao cho \(\sigma\) đồng nhất các phần tử trên \(F\).

Khi đó ta có định lí quan trọng sau về số phần tử của nhóm Galois. Phần chứng minh hiện tại mình bỏ qua vì cần một vài bổ đề khá dài.

Định lí 6.1

Đặt \(f(x)\) là đa thức trên \(F[x]\) và giả sử \(E\) là trường phân rã của \(f(x)\) trên \(F\). Nếu \(f(x)\) không có nghiệm bội thì

\[\lvert G(E/F) \rvert = [E : F].\]