Lý thuyết đồ thị

Phần này mình sử dụng các quyển sách dành cho học sinh chuyên Tin [12].

Các định nghĩa cơ bản

Định nghĩa 27 (Đồ thị)

Đồ thị (hay graph, hay граф) \(G = (V, E)\) gồm một tập hợp các đỉnh \(V\) và tập hợp các cạnh \(E\) nối các đỉnh với nhau.

Đồ thị vô hướng

Ví dụ 21

Đồ thị sau có:

  1. Tập hợp các đỉnh

\[V = \{ v_1, v_2, v_3, v_4, v_5, v_6 \}.\]

  1. Tập hợp các cạnh

\[E = \{ e_{12}, e_{23}, e_{24}, e_{26}, e_{56} \}.\]
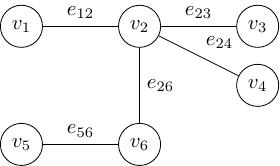
../../_images/undirected-graph.jpg

Hình 4 Đồ thị vô hướng

Ở ví dụ trên, cạnh \(e_{ij}\) nối đỉnh \(v_i\) và đỉnh \(v_j\). Trong trường hợp này hướng của cạnh không quan trọng nên việc viết \(e_{ij}\) và \(e_{ji}\) là tương đương. Đồ thị lúc này gọi là đồ thị vô hướng (hay undirected graph).

Hai đỉnh được gọi là kề nhau (hay adjacent) nếu có cạnh nối giữa chúng.

Ở ví dụ trên thì hai đỉnh \(v_1\) và \(v_2\) kề nhau, nhưng đỉnh \(v_1\) không kề với \(v_3\) vì không có cạnh \(e_{13}\).

Khi đó cạnh nối hai đỉnh kề nhau được gọi là cạnh liên thuộc (hay incident).

Ở đồ thị vô hướng, ta nói bậc (hay degree) của đỉnh \(v\) là số cạnh liên thuộc với đỉnh \(v\), và kí hiệu là \(\deg (v)\).

Ở Hình 4 ta thấy \(\deg (v_1) = 1\), \(\deg (v_2) = 3\), \(\deg (v_3) = 1\), \(\deg (v_4) = 1\), \(\deg (v_5) = 1\), \(\deg (v_6) = 2\). Tổng quát ta có định lí sau.

Định lí 8

Giả sử \(G = (V, E)\) là đồ thị vô hướng, khi đó tổng tất cả các bậc của các đỉnh trong \(V\) sẽ bằng hai lần số cạnh:

\[\sum_{v \in V} \deg (v) = 2 \lvert E \rvert.\]

Chứng minh

Khi lấy tổng tất cả các bậc thì mỗi cạnh \(e_{ij}\) sẽ được tính một lần cho đỉnh \(v_i\) và một lần cho đỉnh \(v_j\). Từ đó suy ra kết quả.

Hệ quả 2

Trong đồ thị vô hướng thì số đỉnh có bậc lẻ là số chẵn.

Chứng minh

Giả sử \(v_1\) là tập các đỉnh có bậc lẻ và \(v_2\) là tập các đỉnh có bậc chẵn. Khi đó \(_1 \cup V_2 = V\) và \(V_1 \cap V_2 = \emptyset\). Theo định lí trên thì

\[\sum_{v_1 \in V_1} \deg (v_1) + \sum_{v_2 \in V_2} \deg (v_2) = 2 \lvert E \rvert\]

là số chẵn, mà tổng bậc của các đỉnh bậc chẵn \(\sum\limits_{v_2 \in V_2} \deg (v_2)\) cũng là số chẵn nên suy ra tổng \(\sum\limits_{v_1 \in V_1} \deg (v_1)\) cũng là chẵn.

Do mỗi giá trị \(\deg (v_1)\) là lẻ với mọi \(v_1 \in V_1\) nên tổng của chúng là chẵn khi và chỉ khi số phần tử của \(v_1\) là chẵn. Ta có điều phải chứng minh.

Đồ thị có hướng

Nếu chúng ta quan tâm đến hướng thì khi vẽ cạnh \(e_{ij}\) ta vẽ mũi tên từ đỉnh \(v_i\) tới đỉnh \(v_j\). Đồ thị khi đó gọi là đồ thị có hướng (hay directed graph).

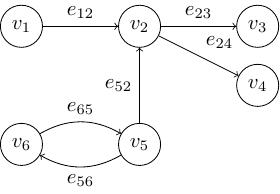
../../_images/directed-graph.jpg

Hình 5 Đồ thị có hướng

Ở hình trên:

  • chỉ có cạnh từ \(v_1\) tới \(v_2\) là \(e_{12}\) chứ không có cạnh từ \(v_2\) tới \(v_1\)

  • có cạnh từ \(v_6\) tới \(v_5\) là \(e_{65}\) và cũng có cạnh từ \(v_5\) tới \(v_6\) là \(e_{56}\).

Lúc này tập đỉnh là

\[V = \{ v_1, v_2, v_3, v_4, v_5, v_6 \},\]

và tập cạnh là

\[E = \{ e_{12}, e_{23}, e_{24}, e_{52}, e_{56}, e_{65} \}.\]

Đối với đồ thị có hướng thì cạnh \(e_{ij}\) là cạnh đi ra từ đỉnh \(i\) và đi vào đỉnh \(j\). Đỉnh \(i\) gọi là đỉnh đầu, đỉnh \(j\) gọi là đỉnh cuối.

Định nghĩa 28 (Bán bậc vào, bán bậc ra)

Bán bậc ra (hay out-degree) của đỉnh \(v\) là số lượng cạnh đi ra khỏi nó và kí hiệu là \(\deg^+(v)\).

Bán bậc vào (hay in-degree) của đỉnh \(v\) là số lượng cạnh đi vào nó và kí hiệu là \(\deg^-(v)\).

Với ví dụ ở Hình 5 thì:

  • \(\deg^+(v_1) = 1\), \(\deg^-(v_1) = 0\);

  • \(\deg^+(v_2) = 2\), \(\deg^-(v_2) = 1\);

  • \(\deg^+(v_3) = 0\), \(\deg^-(v_3) = 1\);

  • \(\deg^+(v_4) = 0\), \(\deg^-(v_4) = 1\);

  • \(\deg^+(v_5) = 2\), \(\deg^-(v_5) = 1\);

  • \(\deg^+(v_6) = 1\), \(\deg^-(v_6) = 1\).

Định lí 9

Nếu \(G = (V, E)\) là đồ thị có hướng thì tổng tất cả các bán bậc ra của các đỉnh bằng tổng tất cả các bán bậc vào, và cũng bằng tổng số cung của đồ thị

\[\sum_{v \in V} \deg^+(v) = \sum_{v \in V} \deg^-(v) = \lvert E \rvert.\]

Chứng minh

Mỗi cạnh của đồ thị đi ra từ đúng một đỉnh nên \(\sum\limits_{v \in V} \deg^+(v) = \lvert E \rvert\).

Tương tự, mỗi cạnh của đồ thị đi vào đúng một đỉnh nên \(\sum\limits_{v \in V} \deg^-(v) = \lvert E \rvert\).

Kết hợp hai đẳng thức trên ta có điều phải chứng minh.

Đường đi và chu trình

Một dãy có thứ tự các đỉnh \(v_{i_0}\), \(v_{i_1}\), ..., \(v_{i_n}\) sao cho \(e_{i_t i_{t+1}} \in E\) với mọi \(t = 0, 1, \ldots, n-1\) được gọi là đường đi. Lúc này đường đi có \(n+1\) đỉnh \(v_{i_0}\), \(v_{i_1}\), ..., \(v_{i_n}\) và \(n\) cạnh \(e_{i_0 i_1}\), \(e_{i_1 i_2}\), ..., \(e_{i_{n-1} i_n}\).

Nếu tồn tại một đường đi từ đỉnh \(v_{i_0}\) tới đỉnh \(v_{i_n}\) thì ta nói đỉnh \(v_{i_n}\) đến được (hay reachable) từ đỉnh \(v_{i_0}\) và kí hiệu là \(v_{i_0} \leadsto v_{i_n}\).

  1. Đỉnh \(v_{i_0}\) được gọi là đỉnh đầu của đường đi.

  2. Đỉnh \(v_{i_n}\) được gọi là đỉnh cuối của đường đi.

  3. Các đỉnh \(v_{i_1}\), ..., \(v_{i_{n-1}}\) được gọi là đỉnh trong của đường đi.

Đường đi được gọi là đường đi đơn (hay simple) nếu tất cả các đỉnh trên đường đi hoàn toàn phân biệt.

Hình 6 thể hiện hai đường đi đơn từ đỉnh \(v_1\) tới đỉnh \(v_3\):

  • đường đi thứ nhất là \(v_1\), tới \(v_2\) và tới \(v_3\)

  • đường đi thứ hai là \(v_1\), tới \(v_2\), đi xuống \(v_4\), đi lên \(v_6\) và quay lại \(v_3\).

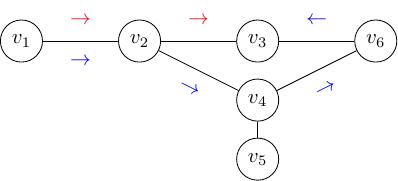
../../_images/path.jpg

Hình 6 Đường đi từ \(v_1\) tới \(v_3\)

Đường đi được gọi là chu trình (hay circuit) nếu đỉnh đầu trùng với đỉnh cuối, nghĩa là \(v_{i_0} = v_{i_n}\).

Đẳng cấu đồ thị

Định nghĩa 29

Hai đồ thị \(G = (V, E)\) và \(G' = (V', E')\) được gọi là đẳng cấu (hay isomorphic) nếu tồn tại một song ánh \(f : V \to V'\) sao cho số cung nối đỉnh \(u\) với đỉnh \(v\) trên \(E\) bằng số cung nối đỉnh \(f(u)\) với đỉnh \(f(v)\) trên \(E'\).

Nói cách khác, kí hiệu \(e_{ij}\) là cạnh nối đỉnh \(v_i\) và \(v_j\) trên \(E\). Đặt \(v_i' = f(v_i)\) và \(v_j' = f(v_j)\) là các đỉnh thuộc \(V'\). Khi đó \(e_{ij}'\) là cạnh thuộc \(E'\) nối đỉnh \(v'_i\) và đỉnh \(v'_j\). Nếu giữa \(v_i\) và \(v_j\) không có cạnh nào thì cũng không có cạnh nối \(v_i'\) và \(v_j'\).

Bài toán đẳng cấu đồ thị (graph isomorphism problem) là một trong những bài toán khó hiện nay (tháng 1 năm 2025) về việc tìm lời giải trong thời gian đa thức. Nếu cho trước hai đồ thị thì nhiệm vụ của bài toán là xác định xem hai đồ thị có đẳng cấu hay không. Rõ ràng nếu số đỉnh nhỏ thì chúng ta có thể thử từng hoán vị (song ánh) của tập đỉnh, nhưng khi số đỉnh lớn thì việc thử sai tất cả hoán vị là không thể.

Đồ thị con

Định nghĩa 30 (Đồ thị con)

Đồ thị \(G' = (V', E')\) là đồ thị con (hay subgraph, hay подграф) của đồ thị \(G = (V, E)\) nếu \(V' \subseteq V\) và \(E' \subseteq E\).

Nói cách khác, đồ thị con thu được từ đồ thị ban đầu bằng việc lấy một lượng nhất định đỉnh và cạnh.

Ở đồ thị trên Hình 7, mình lấy các đỉnh \(v_1\), \(v_2\), \(v_4\) và \(v_5\), và lấy các cạnh \(e_{24}\), \(e_{45}\) thì mình có đồ thị con trên Hình 8. Các bạn có thể thấy ở đồ thị ban đầu thì \(v_1\) nối với \(v_2\), nhưng ở đồ thị con thì không có cạnh nối giữa hai đỉnh này.

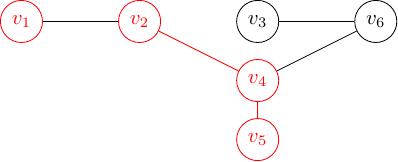
../../_images/subgraph-1.jpg

Hình 7 Đồ thị ban đầu

../../_images/subgraph-2.jpg

Hình 8 Đồ thị con

Đồ thị đầy đủ

Đồ thị vô hướng được gọi là đầy đủ (hay complete, hay полный) nếu mọi cặp đỉnh đều kề nhau.

Đồ thị đầy đủ gồm \(n\) đỉnh kí hiệu là \(K_n\).

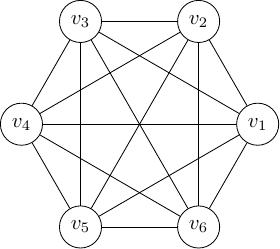
../../_images/complete-graph.jpg

Hình 9 Ví dụ \(K_6\)

Dễ thấy số cạnh của đồ thị đầy đủ \(n\) đỉnh là \(C^2_n\).

Đồ thị hai phía

Đồ thị vô hướng được gọi là hai phía (hay bipartite) nếu tập đỉnh của nó có thể chia thành hai tập rời nhau \(V_1\) và \(V_2\) sao cho không tồn tại cạnh nối hai đỉnh của \(V_1\), và cũng không tồn tại cạnh nối hai đỉnh của \(V_2\).

Nếu \(\lvert V_1 \rvert = n_1\) và \(\lvert V_2 \rvert = n_2\) và giữa mọi cặp đỉnh \((v_1, v_2)\), trong đó \(v_1 \in V_1\) và \(v_2 \in V_2\), đều có cạnh nối thì đồ thị hai phía đó được gọi là đồ thị hai phía đầy đủ, kí hiệu là \(K_{v_1, v_2}\).

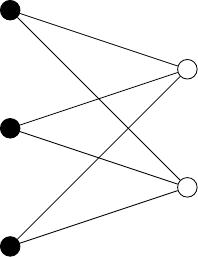
../../_images/bipartite.jpg

Hình 10 Ví dụ đồ thị hai phía đầy đủ \(K_{3, 2}\)

Theo quy tắc nhân, số cạnh của đồ thị hai phía đầy đủ là \(v_1 \cdot v_2\) vì mỗi đỉnh ở \(V_1\) đều có \(v_2\) cạnh nối với nó, và có tất cả \(v_1\) đỉnh trong \(V_1\).

Đồ thị phẳng

Đồ thị được gọi là đồ thị phẳng (hay planar graph, hay планарный граф) nếu chúng ta có thể vẽ đồ thị trên mặt phẳng sao cho:

  1. Mỗi đỉnh tương ứng với một điểm trên mặt phẳng, không có hai đỉnh cùng tọa độ.

  2. Mỗi cạnh tương ứng với một đường liên tục nối hai đỉnh và hai cạnh bất kì không giao nhau.

Phép vẽ đồ thị phẳng này được gọi là biểu diễn phẳng của đồ thị.

Định lí 10 (Định lí Kuratowski)

Một đồ thị vô hướng là đồ thị phẳng khi và chỉ khi nó không chứa đồ thị con đẳng cấu với \(K_{3, 3}\) hoặc \(K_5\).

Định lí 11 (Công thức Euler)

Nếu một đồ thị vô hướng liên thông là đồ thị phẳng và biểu diễn phẳng của đồ thị đó gồm \(v\) đỉnh và \(e\) cạnh chia mặt phẳng thành \(f\) phần thì

\[v - e + f = 2.\]

Công thức Euler này chúng ta cũng thấy ở hình học không gian đối với một khối đa diện. Nếu \(v\) là số đỉnh (vertices), \(e\) là số cạnh (edges) và \(f\) là số mặt (faces) thì \(v - e + f = 2\).

  1. Hình tứ diện có \(4\) đỉnh, \(6\) cạnh và \(4\) mặt nên \(4 - 6 + 4 = 2\).

  2. Hình lập phương có \(8\) đỉnh, \(12\) cạnh và \(6\) mặt nên \(8 - 12 + 6 = 2\).

Định lí 12

Nếu đồ thị vô hướng \(G = (V, E)\) là đồ thị phẳng có ít nhất \(3\) đỉnh thì

\[\lvert E \rvert \leqslant 3 \lvert V \rvert - 6.\]

Ngoài ra nếu \(G\) không có chu trình độ dài \(3\) thì

\[\lvert E \rvert \leqslant 2 \lvert V \rvert - 4.\]

Tính liên thông của đồ thị

Tính liên thông trên đồ thị vô hướng

Định nghĩa 31 (Đồ thị liên thông)

Một đồ thị vô hướng được gọi là liên thông (hay connected, hay связанный) nếu giữa hai đỉnh bất kì của đồ thị tồn tại đường đi.

Đồ thị chỉ gồm một đỉnh duy nhất cũng được coi là đồ thị liên thông.

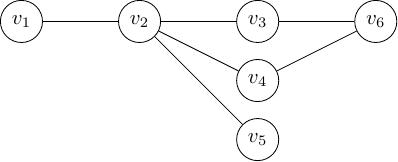
../../_images/connected-graph.jpg

Hình 11 Đồ thị liên thông

Định nghĩa 32 (Thành phần liên thông)

Cho đồ thị \(G = (V, E)\). Nếu đồ thị con \(G' = (V', E')\) của \(G\) là đồ thị liên thông thì \(G'\) được gọi là thành phần liên thông (hay connected component, связанный компонент) của đồ thị \(G\).

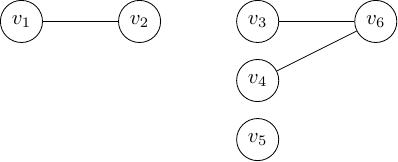
../../_images/connected-component.jpg

Hình 12 Các thành phần liên thông trên đồ thị

Trên Hình 12 có ba thành phần liên thông:

  • thành phần liên thông thứ nhất gồm hai đỉnh \(v_1\), \(v_2\), và cạnh \(e_{12}\)

  • thành phần liên thông thứ hai gồm ba đỉnh \(v_3\), \(v_4\), \(v_6\), và các cạnh \(e_{36}\), \(e_{46}\)

  • thành phần liên thông thứ ba chỉ gồm đỉnh \(v_5\).

Đôi khi việc bỏ đi một đỉnh và tất cả cạnh liên thuộc với nó sẽ tăng số lượng thành phần liên thông hơn so với đồ thị ban đầu. Các đỉnh như vậy gọi là đỉnh cắt (hay cut vertices), hoặc nút khớp (hay articulation nodes).

Tương tự, khi bỏ đi một cạnh mà số lượng thành phần liên thông tăng lên thì cạnh đó gọi là cạnh cắt (hay cut edges) hoặc cầu (hay bridge).

Ở Hình 13 là một đồ thị liên thông, nếu chúng ta xóa cạnh \(e_{24}\) (cạnh màu đỏ) thì chúng ta sẽ có hai thành phần liên thông:

  • thành phần liên thông thứ nhất gồm hai đỉnh \(v_1\) và \(v_2\)

  • thành phần liên thông thứ hai gồm bốn đỉnh \(v_3\), \(v_4\), \(v_5\) và \(v_6\).

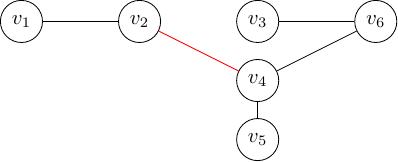
../../_images/bridge.jpg

Hình 13 Ví dụ về cầu

Đồ thị có thể có nhiều cầu. Ở Hình 13, thay vì xóa cạnh \(e_{24}\), nếu ta xóa cạnh \(e_{46}\) thì cũng làm tăng số thành phần liên thông. Do đó cạnh \(e_{46}\) cũng là cầu. Tương tự cho cạnh \(e_{12}\), ...

Tính liên thông trên đồ thị có hướng

Một đồ thị có hướng được gọi là:

  • liên thông mạnh (hay strongly connected) nếu tồn tại đường đi giữa hai đỉnh bất kì của đồ thị;

  • liên thông yếu (hay weakly connected) nếu phiên bản vô hướng của nó là đồ thị liên thông.

Bài toán xác định các thành phần liên thông

Bài toán xác định các thành phần liên thông của đồ thị là một bài toán quan trọng trong lý thuyết đồ thị. Bài toán sẽ tìm tất cả thành phần liên thông của đồ thị vô hướng.

Để liệt kê các thành phần liên thông của đồ thị vô hướng \(G = (V, E)\) ta thực hiện các bước sau:

  1. Bắt đầu từ một đỉnh bất kì, ta tìm tất cả đỉnh đến được từ đỉnh đó. Như vậy chúng ta tìm được một thành phần liên thông.

  2. Loại những đỉnh ở thành phần liên thông đầu tiên và xét một trong những đỉnh còn lại. Lặp lại công việc ở bước 1, ta tìm tất cả đỉnh đến được từ đỉnh đang xét. Như vậy chúng ta tìm được thêm một thành phần liên thông.

  3. Thực hiện đến khi đã xét hết tất cả đỉnh trong đồ thị.

Ở đây, để tìm tất cả đỉnh đến được từ một đỉnh nào đó trong đồ thị ta sử dụng thuật toán DFS (Depth First Search, Duyệt Sâu) hoặc BFS (Breadth First Search, Duyệt Rộng).

Cây

Định nghĩa 33 (Cây)

Cây (hay tree, hay дерево) là đồ thị vô hướng, liên thông, và không có chu trình đơn.

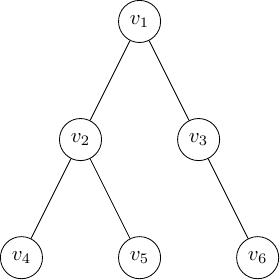
../../_images/tree.jpg

Hình 14 Ví dụ về cây

Định nghĩa 34 (Cây khung)

Xét đồ thị \(G = (V, E)\) và \(T = (V', E')\) là đồ thị con của \(G\). Nếu \(T\) là cây thì ta gọi \(T\) là cây khung hoặc cây bao trùm (hay spanning tree) của đồ thị \(G\).

Điều kiện cần và đủ để một đồ thị vô hướng có cây khung là đồ thị đó phải liên thông.

Một đồ thị có thể có nhiều cây khung. Ở Hình 15 ta xóa đi cạnh \(e_{23}\) và \(e_{46}\) (hai cạnh màu đỏ) thì thu được một cây khung. Tương tự, ở Hình 16 ta xóa đi hai cạnh màu đỏ là \(e_{13}\) và \(e_{23}\) thì cũng thu được một cây khung khác.

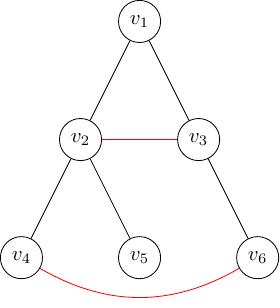
../../_images/spanning-tree-1.jpg

Hình 15 Cây khung thứ nhất

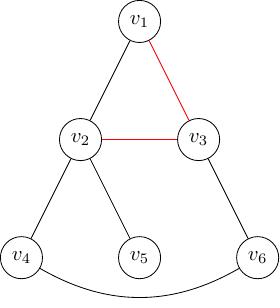
../../_images/spanning-tree-2.jpg

Hình 16 Cây khung thứ hai

Định lí 13 (Daisy Chain Theorem)

Giả sử \(T = (V, E)\) là đồ thị vô hướng với \(n\) đỉnh. Khi đó các mệnh đề sau tương đương:

  1. \(T\) là cây.

  2. \(T\) không chứa chu trình đơn và có \(n - 1\) cạnh.

  3. \(T\) liên thông và mỗi cạnh của nó đều là cầu.

  4. Giữa hai đỉnh bất kì của \(G'\) đều tồn tại đúng một đường đi đơn.

  5. \(T\) không chứa chu trình đơn nhưng nếu ta thêm vào một cạnh thì ta thu được chu trình đơn.

  6. \(T\) liên thông và có \(n - 1\) cạnh.

Các mệnh đề trên có thể xem như các định nghĩa tương đương của cây. Trong nhiều trường hợp thì tính chất của cây có thể thu được từ các định nghĩa này nên mình sẽ chứng minh chuỗi mệnh đề này.

Chứng minh 1 \(\Rightarrow\) 2

Từ \(T\) là cây, theo định nghĩa thì \(T\) không chứa chu trình đơn. Ta chứng minh cây \(T\) có \(n\) đỉnh thì sẽ có \(n - 1\) cạnh bằng quy nạp.

Với \(n = 1\) thì cây chỉ có thể có \(0\) cạnh (không nối đi đâu cả).

Giả thiết quy nạp: với \(n \geqslant 1\) thì cây \(T\) với \(n\) đỉnh có \(n - 1\) cạnh. Đặt các đỉnh là \(v_1\), \(v_2\), ..., \(v_n\).

Bây giờ ta thêm đỉnh \(v_{n+1}\) vào cây \(T\) để được cây mới \(T'\). Ta cần chứng minh cây mới có \(n\) cạnh.

Do \(T\) liên thông nên giữa mọi cặp đỉnh \(u\) và \(v\) của \(T\) đều có đường đi, giả sử là

\[u = v_{i_1} \to v_{i_2} \to \cdots \to v_{i_k} = v.\]

Khi đó, nếu cả hai đỉnh \(u\) và \(v\) đều có cạnh nối với \(v_{n+1}\) thì ta thu được chu trình

\[v_{n+1} \to u = v_{i_1} \to v_{i_2} \to \cdots \to v_{i_k} = v \to v_{n+1},\]

như vậy sẽ không tạo thành cây. Nghĩa là từ \(v_{n+1}\) chỉ có thể nối với một trong các đỉnh \(v_1\), ..., \(v_n\) nên số cạnh chỉ có thể tăng lên \(1\) để có được cây mới. Khi đó, với \(n + 1\) đỉnh ta có \(n\) cạnh, theo quy nạp ta có điều phải chứng minh.

Chứng minh 2 \(\Rightarrow\) 3

Giả sử \(T\) có \(k\) thành phần liên thông \(T_1\), \(T_2\), ..., \(T_k\). Vì \(T\) không chứa chu trình đơn nên các thành phần liên thông của \(T\) cũng không chứa chu trình đơn, tức là \(T_1\), \(T_2\), ..., \(T_k\) đều là cây.

Gọi \(n_1\), \(n_2\), ..., \(n_k\) lần lượt là số đỉnh của \(T_1\), \(T_2\), ..., \(T_k\) thì

  • \(n_1 + \cdots + n_k = n\);

  • cây \(T_1\) có \(n_1 - 1\) cạnh (từ chứng minh 1 \(\Rightarrow\) 2), tương tự cây \(T_2\) có \(n_2 - 1\) cạnh, ..., \(T_k\) có \(n_k - 1\) cạnh.

Cộng số lượng cạnh của \(k\) cây lại ta có tổng số cạnh của cây \(T\), kết hợp giả thiết ban đầu ta có

\[n_1 + n_2 + \cdots + n_k - k = n -k = n - 1.\]

Như vậy \(k = 1\), nghĩa là \(T\) liên thông. Từ đây, do \(T\) không có chu trình nên nếu bỏ một cạnh bất kì thì đồ thị mới cũng không có chu trình. Đồ thị mới không thể liên thông vì nếu giả sử ngược lại (phản chứng) đồ thị mới liên thông thì nó sẽ phải là cây có \(n\) đỉnh. Nhưng hiện tại đồ thị chỉ có \(n - 2\) cạnh vì đã bỏ đi một cạnh, không phải \(n - 1\). Do đó cạnh bỏ đi là cầu.

Chứng minh 3 \(\Rightarrow\) 4

Gọi \(u\) và \(v\) là hai đỉnh bất kì trong \(T\). Vì \(T\) liên thông nên sẽ có một đường đi đơn từ \(u\) tới \(v\) là

\[u = v_{i_1} \to v_{i_2} \to \cdots \to v_{i_k} = v.\]

Giả sử tồn tại một đường đi đơn khác từ \(u\) tới \(v\) là

\[u = v_{j_1} \to v_{j_2} \to \cdots \to v_{j_l} = v.\]

Khi đó nếu ta xóa đi một cạnh ở đường đi đơn đầu nhưng không nằm trên đường đi đơn thứ hai thì \(u\) vẫn tới được \(v\) nhờ vào đường đi đơn thứ hai. Nói cách khác \(u\) và \(v\) vẫn liên thông nên dữ kiện "mọi cạnh đều là cầu" mâu thuẫn.

Nói rõ hơn, không mất tính tổng quát, giả sử đường đi đơn thứ nhất và thứ hai có cạnh chung là \(v_{i_2} \to v_{i_3}\), nghĩa là \(v_{i_2} = v_{j_2}\) và \(v_{i_3} = v_{j_3}\). Khi đó nếu ta xóa cạnh \(v_{i_2} \to v_{i_3}\) thì \(u\) vẫn tới được \(v\) và số lượng thành phần liên thông không tăng.

Chứng minh 4 \(\Rightarrow\) 5

Cây \(T\) sẽ không chứa chu trình đơn vì khi đó sẽ có hai đường đi đơn từ hai điểm bất kì trên chu trình đó (chúng ta có thể tưởng tượng đi cùng chiều và ngược chiều kim đồng hồ đều có thể đi từ 1 tới 3).

Khi đó, hai đỉnh bất kì \(u\) và \(v\) luôn liên thông, nghĩa là tồn tại đường đi

\[u = v_{i_1} \to v_{i_2} \to \cdots \to v_{i_k} = v.\]

Nếu ta thêm bất kì bất kì cạnh nào nối giữa hai đỉnh trên đường đi, không mất tính tổng quát giả sử là \(v_{i_1}\) và \(v_{i_k}\), khi đó ta có chu trình vì

\[u = v_{i_1} \to v_{i_2} \to \cdots \to v_{i_k} = v \to v_{i_1}.\]

Như vậy cứ thêm vào một cạnh ta sẽ có chu trình.

Chứng minh 5 \(\Rightarrow\) 6

Giữa hai đỉnh bất kì \(u\) và \(v\) của \(T\) có hai trường hợp:

  • \(u\) và \(t\) được nối bởi một cạnh;

  • \(u\) và \(t\) không kề nhau (không có cạnh nối). Ở trường hợp này, nếu chúng ta vẽ cạnh nối \(u\) với \(v\) thì theo giả thiết sẽ tạo ra chu trình. Điều này chỉ xảy ra khi và chỉ khi có một đường đi đơn từ \(u\) tới \(v\).

Như vậy trong cả hai trường hợp thì luôn tồn tại đường đi từ \(u\) tới \(v\), nói cách khác là hai đỉnh liên thông. Điều này đúng với mọi đỉnh trong đồ thị nên \(T\) liên thông.

Do ta đã chứng minh được \(T\) liên thông, và giả thiết là \(T\) không chứa chu trình đơn, nên suy ra \(T\) là cây. Như vậy \(T\) có \(n - 1\) cạnh.

Chứng minh 6 \(\Rightarrow\) 1

Sử dụng phản chứng, giả sử \(T\) không là cây. Khi đó \(T\) không liên thông hoặc \(T\) có chu trình. Do giả thiết \(T\) liên thông nên ta chỉ xét trường hợp \(T\) có chu trình.

Nếu ta bỏ một cạnh trên chu trình này thì \(T\) vẫn liên thông. Nếu \(T\) vẫn còn chu trình thì ta lại bỏ đi một cạnh của chu trình đó. Tiếp tục cho đến khi \(T\) không còn chu trình nào. Lúc này \(T\) là cây nhưng lại có ít hơn \(n - 1\) cạnh do chúng ta đã bỏ ít nhất một cạnh. Điều này vô lí vì ở chứng minh trên (1 \(\Rightarrow\) 2), nếu \(T\) là cây thì \(T\) có \(n - 1\) cạnh. Như vậy theo phản chứng suy ra \(T\) là cây.

Định lí 14

Số cây khung của đồ thị đầy đủ \(K_n\) là \(n^{n-2}\).

Đồ thị Euler và đồ thị Hamilton

Đồ thị Euler

Leonhard Euler là người đầu tiên mô hình hóa bài toán rời rạc này thành một hệ thống hoàn chỉnh là Lý thuyết đồ thị hiện nay.

Định nghĩa 35 (Chu trình Euler)

Chu trình đi qua tất cả các cạnh của đồ thị, mỗi cạnh đúng một lần, được gọi là chu trình Euler (hay Euler circuit, Euler circle, Euler tour).

Định nghĩa 36 (Đường đi Euler)

Đường đi đi qua tất cả các cạnh của đồ thị, mỗi cạnh đúng một lần, được gọi là đường đi Euler.

Lúc này, bài toán \(7\) cây cầu nổi tiếng của thành phố Konigsberg (nay là thành phố Kaliningrad thuộc Liên bang Nga) trở thành bài toán xác định xem có tồn tại chu trình Euler hay không.

Định nghĩa 37 (Đồ thị Euler)

Đồ thị có chu trình Euler được gọi là đồ thị Euler (hay Eulerian graph, unicursal graph).

Định nghĩa 38 (Đồ thị nửa Euler)

Đồ thị có đường đi Euler được gọi là đồ thị nửa Euler (hay Semi-Eulerian graph, Traversable graph).

Các định lí và thuật toán trên đồ thị Euler

Định lí 15

Một đồ thị vô hướng liên thông \(G = (V, E)\) có chu trình Euler khi và chỉ khi mọi đỉnh của nó đều có bậc chẵn.

[TODO] Chứng minh

Chiều thuận. Nếu \(G\) có chu trình Euler thì khi đi theo chu trình đó, mỗi đỉnh sẽ đi vào một lần và đi ra một lần nên bậc của nó tăng lên \(2\). Áp dụng cho mỗi lần gặp một đỉnh thì cuối cùng bậc của mỗi đỉnh phải là số chẵn

[TODO] Chiều ngược. Nếu mọi đỉnh của đồ thị đều có bậc chẵn, ta cần xây dựng cách tìm chu trình Euler.

Hệ quả 3

Một đồ thị vô hướng liên thông \(G = (V, E)\) có đường đi Euler khi và chỉ khi nó có đúng hai đỉnh bậc lẻ.

Chứng minh

Điều kiện của đường đi Euler "lỏng hơn" chu trình vì điểm đầu không cần phải trùng với điểm cuối. Do đó nếu \(G\) có đường đi Euler thì đỉnh bắt đầu và kết thúc sẽ có bậc lẻ, các đỉnh còn lại có bậc chẵn. Ngược lại nếu đồ thị liên thông có đúng hai đỉnh bậc lẻ, khi đó ta vẽ cạnh nối hai đỉnh đó thì tất cả đỉnh của đồ thị đều có bậc chẵn, nghĩa là tồn tại chu trình Euler. Loại bỏ cạnh đó thì ta có đường đi Euler.

[TODO] Chu trình Euler và đường đi Euler của đồ thị có hướng liên thông yếu.

Đồ thị Hamilton

Khái niệm đường đi và chu trình Hamilton được đưa ra bởi William Rowan Hamilton (1856).

Định nghĩa 39 (Chu trình Hamilton và đồ thị Hamilton)

Đồ thị \(G = (V, E)\) được gọi là đồ thị Hamilton (hay Hamilton graph) nếu tồn tại chu trình đơn đi qua tất cả các đỉnh.

Chu trình đơn đi qua tất cả các đỉnh gọi là chu trình Hamilton (hay Hamiltonian circuit, Hamilton circle).

Người ta quy ước rằng đồ thị chỉ gồm một đỉnh là đồ thị Hamilton nhưng đồ thị gồm hai đỉnh liên thông không phải là đồ thị Hamilton.